15. Алгебраические уравнения И Алгебраические неравенства. Уравнения высших степеней
Уравнение вида
![]() (3.1)
(3.1)
Где ![]() называется Уравнением N-й степени.
называется Уравнением N-й степени.
Если ![]() уравнение
уравнение ![]() называется Линейным.
называется Линейным.
Если ![]() уравнение
уравнение ![]() называется Квадратным.
называется Квадратным.
Если ![]() уравнение называется Однородным.
уравнение называется Однородным.
Основными методами решения уравнений типа (3.1) при ![]() являются:
являются:
1) метод разложения многочлена в левой части уравнения (3.1) на множители и сведение к равносильной совокупности уравнений;
2) метод замены переменной, в результате применения которого уравнение (3.1) заменяется равносильным уравнением, степень которого ниже, чем N;
3) поиск корней среди делителей свободного члена.
Рассмотрим некоторые виды уравнений (3.1) и их решения.
Уравнения вида ![]() решаются вынесением общего множителя
решаются вынесением общего множителя ![]() за скобки:
за скобки:
![]()
И сведением к совокупности:
![]()
Уравнение вида
![]()
![]() (3.2)
(3.2)
Решается заменой ![]() Получаем уравнение
Получаем уравнение ![]() которое решается, как квадратное. Находим его корни (если такие существуют) и возвращаемся к старой переменной.
которое решается, как квадратное. Находим его корни (если такие существуют) и возвращаемся к старой переменной.
При ![]() уравнение (3.2) имеет вид:
уравнение (3.2) имеет вид:
![]() – Биквадратное уравнение.
– Биквадратное уравнение.
Уравнение
![]() (3.3)
(3.3)
Где ![]() сводится к биквадратному уравнению заменой
сводится к биквадратному уравнению заменой ![]()
Уравнение
![]() (3.4)
(3.4)
Где ![]() и А таковы, что
и А таковы, что ![]() и
и ![]() сводится к биквадратному уравнению заменой
сводится к биквадратному уравнению заменой
![]()
Или при ![]() к уравнению
к уравнению
![]()
Заменой
![]()
Уравнение
![]() (3.5)
(3.5)
Где ![]() и
и ![]() делением на
делением на ![]() (так как
(так как ![]() – не является корнем) сводится к равносильному ему уравнению:
– не является корнем) сводится к равносильному ему уравнению:
![]()
Далее заменой ![]() оно сводится к квадратному уравнению.
оно сводится к квадратному уравнению.
Уравнение
![]()
Где ![]() и А таковы, что
и А таковы, что ![]() сводится к уравнению вида (3.5) после попарного перемножения выражений в скобках:
сводится к уравнению вида (3.5) после попарного перемножения выражений в скобках:
![]()
Уравнения вида
![]() (3.6)
(3.6)
Где ![]() называются Симметрическими уравнениями третьей степени.
называются Симметрическими уравнениями третьей степени.
Так как
![]()
То уравнение (3.5) равносильно совокупности уравнений:
![]()
Уравнения вида
![]() (3.7)
(3.7)
Где ![]() называются Симметрическими уравнениями четвертой степени.
называются Симметрическими уравнениями четвертой степени.
Так как ![]() не является корнем уравнения (3.7), то деление обеих частей уравнения (3.7) на
не является корнем уравнения (3.7), то деление обеих частей уравнения (3.7) на ![]() приводит его к уравнению
приводит его к уравнению
![]() или
или
![]()
Далее заменяем ![]() и сводим его к квадратному уравнению.
и сводим его к квадратному уравнению.
Пример 1. Решить уравнение ![]()
Решение. Выносим общий множитель за скобки:
![]()
Получаем совокупность уравнений
![]()
Ее решение дает три корня:
![]()
Пример 2. Решить уравнение
![]()
Решение. Заменяем ![]() и приходим к уравнению
и приходим к уравнению
![]()
Последнее уравнение имеет корни:
![]()
Возвращаемся к переменной Х:
![]()
Решаем полученные квадратные уравнения и приходим к ответу:
![]()
Пример 3. Решить уравнение ![]()
Решение. Задано уравнение вида (3.3). Заменяем
![]() т. е.
т. е. ![]() Подставим это значение в заданное уравнение:
Подставим это значение в заданное уравнение:
![]()
После упрощения имеем:
![]()
Дополним до полного квадрата суммы:
![]()
После упрощения уравнение приобретает вид:
![]() т. е.
т. е. ![]()
Его решением является лишь ![]()
Возвращаясь к переменной Х, получим ![]() что приводит к ответу:
что приводит к ответу: ![]()
Пример 4. Решить уравнение ![]()
Решение. Имеем уравнение вида (3.4).
Так как ![]() то перемножим выражения во 2-й и 3-й скобках. Получим:
то перемножим выражения во 2-й и 3-й скобках. Получим:
![]()
Заменяем ![]()
Поскольку ![]() приходим к уравнению
приходим к уравнению
![]()
Решая его как квадратное, получим корни:
![]()
Возвращаемся к переменной Х:
![]()
Первое квадратное уравнение полученной совокупности не имеет корней, так как ![]() а второе имеет корни
а второе имеет корни ![]() что и будет ответом.
что и будет ответом.
Пример 5. Решить уравнение ![]()
Решение. Имеем уравнение вида (3.5). Поскольку ![]() не является его корнем (в чем можно убедиться подстановкой), то делим его почленно на
не является его корнем (в чем можно убедиться подстановкой), то делим его почленно на ![]() Получаем
Получаем
![]()
Введем замену ![]() которая приводит к уравнению
которая приводит к уравнению
![]() т. е.
т. е. ![]()
Находим корни ![]() и возвращаемся к переменной Х:
и возвращаемся к переменной Х:
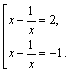
Решаем полученную совокупность дробно-рациональных уравнений:
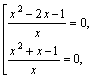 т. е.
т. е. ![]()
Получаем в совокупности 4 корня:
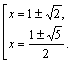
Пример 6. Решить уравнение ![]()
Решение. Это уравнение 3-й степени. Разложим на множители многочлен в правой части. Для этого рассмотрим делители свободного члена 16:
![]()
Подстановкой находим, что ![]() – корень этого многочлена. Следовательно, многочлен разделится нацело на
– корень этого многочлена. Следовательно, многочлен разделится нацело на ![]()
Воспользуемся правилом «деления углом»:
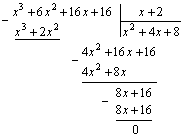
Данное уравнение равносильно уравнению
![]()
Решение которого сводится к совокупности
![]()
Квадратное уравнение не имеет корней, а поэтому получаем единственный корень ![]()
Пример 7. Решить уравнение ![]()
Решение. Данное уравнение является симметрическим уравнением 4-й степени вида (3.7). Поскольку ![]() не является его корнем, то делим это уравнение почленно на
не является его корнем, то делим это уравнение почленно на ![]() Приходим к уравнению
Приходим к уравнению
![]()
Заменяем
![]()
Соответственно,
![]() и
и ![]()
Приходим к уравнению вида
![]() т. е.
т. е. ![]()
Находим корни:
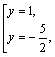
И возвращаемся к переменной Х:
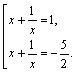
После упрощения получаем:
![]()
При этом первое уравнение последней совокупности не имеет корней, а второе имеет два корня:

Что и является ответом.
| < Предыдущая | Следующая > |
|---|