94. Евклидовы пространства. Скалярное произведение в векторных пространствах. Определение, простейшие свойства и примеры евклидова пространства
Рекомендуемая литература
7. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.
8. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. 1997.
9. Воеводин В. В. Линейная алгебра.. М.: Наука 1980.
10. Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А. В., Демидовича Б. П.. М.: Наука, 1981.
11. Бутузов В. Ф., Крутицкая Н. Ч., Шишкин А. А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.
12. Воеводин В. В. Линейная алгебра. М.: Наука, 1980.
1. Скалярное произведение в векторных пространствах. Определение, простейшие свойства и примеры евклидова пространства. Пусть V векторное пространство над полем действительных чисел R
Определение 1. Отображение множества V´V В R, которое каждой упорядоченной паре (A, B) векторов A, B Из V Ставит в соответствие единственное число из R, Обозначаемое (A, B) или Ab,Называется скалярным произведение, Если оно обладает свойствами:
1) (" A€V) aa ³ 0; Aa = 0 Û A = 0;
2) (" A, b €V) ab =ba;
3) (" A, b, c €V) a(B + C) = Ab + ac;
4) (" A, b €V) (" a€R) (aA)B =A(Ab).
Определение 2. Евклидовым пространством называется векторное пространство над полем R, на котором определено скалярное произведение векторов. Обозначаем n - мерное евклидово пространство символом En.
Свойство 1. 0×A = 0.
Доказательство. По свойству векторного пространства 0×B = 0 Для любого B €V . Отсюда по определению 1 и свойствам поля получим:
А×0 = А×(0×B)= (0×B)×А = 0×(B×А) = 0.
Свойство 2. (-A)B = -Ab.
Доказательство. По свойству векторного пространства (-1)×A = -A Для любого A €V . Отсюда по определению 1 и свойствам поля получим:
(-A)× b = ((-1)A)×B= (-1)(А×B) = -А×B = 0.
Свойство 3. ![]() .
.
Доказательство. Действительно, по определению при k = 2 имеем:
(a1A1 + a2A2)B = (a1A1)×B + (a2A2)×B = a1(A1×B) + a2(A2×B),
А в общем случае равенство доказывается методом математической индукции по K.
Пример 1. Покажем, что в любом N-мерном векторном пространстве V Можно ввести скалярное произведение. Пусть V1 ,V2 ,... VN - базис V и произвольные векторы A, b €V разложены по базису.
A = A1V1 + A2V2 +...+ ANVN , B = B1V1 + B2V2 +...+ BNVN.
Определим скалярное произведение по формуле:
Аb = A1B1 + A2B2 + ... + AKBK .
Тогда Аb € Р и определено однозначно. Условие 1° следует из коммутативности умножения чисел в поле Р. Проверяя условие 2° рассмотрим еще вектор С = G1V1 + G2V2 +...+ GNVN. Тогда
A + B = (A1 + B1)V1 + (A2 + BN)V2 + ...+ (AN + BN)VN.
(A + B)C = (A1 + B1)G1 +(A2 + B2)G2 + ...+ (AK + BK)GK =
= (A1G1 +A2G2 + ...+ AKGK) + (B1G1 +B2G2 + ...+ BKGK) = Аb + ac .
Условие 3° проверяется аналогично.
Пример 2. Пространство геометрических векторов R3 является евклидовым пространством, если в нем скалярное произведение векторов ![]() Определено по формуле:
Определено по формуле: ![]() , где
, где ![]() - длины векторов
- длины векторов ![]() ,j - угол между этими векторами. Проверка условий в определениях 1 , 4 производилась в курсе аналитической геометрии.
,j - угол между этими векторами. Проверка условий в определениях 1 , 4 производилась в курсе аналитической геометрии.
Пример 3. Арифметическое N-мерном RN над полем R является евклидовым, если в нем определить скалярное произведение по формуле:
АB = A1B1 + A2B2 + ... + AKBK ,
Где A = (A1, A2, ..., AN), B = (B1, B2, ..., BN) € RN. Проверку условий в определениях 1 , 4 произведите самостоятельно.
Пример 4. Любое N-мерном векторном пространстве V Над полем R является евклидовым, если в нем определить скалярное произведение по формуле:
АB = A1B1 + A2B2 + ... + AKBK ,
Где A = A1V1 + A2V2 +...+ ANVN , B = B1V1 + B2V2 +...+ BNVN разложения векторов A, b €V по некоторому базису V1 ,V2 ,... VN пространства V . Так как ранее (пример 1) было доказано, что это скалярное произведение, то осталось проверить, что Aa > 0 для любого A € V, a ≠ 0. Действительно, если A ≠ 0, то хотя одна из координат A1, A2, ..., AN вектора A неравна нулю и Aa = A12 + + A22 +...+ AN2 > 0.
Пример 5. Пространство С[A,B] непрерывных на отрезке [A,B] фуекций явлется евклидовым пространство, если вввести на нем скалярное произведение по формуле:
![]() . (6)
. (6)
Так как определенный интеграл от непрерывных функций существует, определен однозначно и принадлежит R, то проверим условия в определениях 1 и 5 используя свойства опрераций над функциями и свойства определенного интеграла.
1° 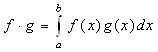 =
=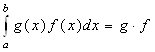 .
.
2° 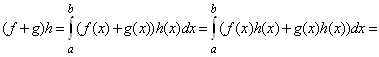
![]() .
.
3° 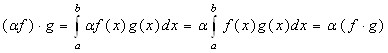 .
.
4° 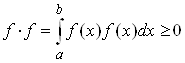 и если F ≠ 0, то F × f > 0.
и если F ≠ 0, то F × f > 0.
| < Предыдущая | Следующая > |
|---|