88. Эквивалентные системы векторов и их свойства

Лемма 1. Пусть S1 , S2 - Конечные системы векторов. Если вектор С линейная комбинация векторов системы S1 И каждый вектор системы S1 Линейная комбинация векторов системы S2 , То вектор С линейная комбинация векторов системы S2 .

Доказательство. Пусть S1 = { a1, A2, ..., AM } , S2 = { b1, B2, ..., BN } . По по условию:

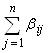С = AI , AI = BJ (I=1, 2,... , M).

Подставляя вторые равенства в первое получим:

С = (BJ) = BJ .

Лемма доказана.

Определение 3. Две конечные системы векторов S1 и S2 называются Эквивалентными, если каждый вектор системы S1 линейная комбинация векторов системы S2 и каждый вектор системы S2 линейная комбинация векторов системы S1.

Эквивалентность систем S1 и S2 обозначается символом S1 ~ S2 .

Теорема 2. Отношение эквивалентности систем векторов рефлексивно, симметрично, транзитивно, т. е. для любых трех систем S1, S2 , S3 Выполняются свойства:

1° S1 ~ S1;

2° Если S1 ~ S2 , То S2 ~ S1;

3° Если S1 ~ S2 и S2 ~ S3 , То S1 ~ S3.

Доказательство. Так как свойства 1° и 2° очевидны, то докажем свойство 3°. Пусть S1 = { a1, A2, ..., AM } , S2 = { b1, B2, ..., BN } , S2 = { c1, C2, ..., CP } . По условию и определению эквивлентности систем векторов каждый вектор AI € S1 линейная комбинация векторов системы S2 и каждый вектор системы S2 линейная комбинация векторов системы S3 , то по лемме Ai линейная комбинация векторов системы S3 . Аналогично доказывается, что каждый вектор СK € S3 линейная комбинация векторов системы S1 . Тогда по определению эквивалентности S1 ~ S3 Свойство доказано.

Теорема 3. Если конечные системы векторов эквивалентны, то их ранги равны.

Доказательство. Пусть S1, S2 две конечные системы векторов, S1 ~ S2. Если какая-нибудь из систем S1 или S2 нулевая, то и другая нулевая и тогда ранги обеих систем равны нулю. Пусть S1 и S2 ненулевые системы и пусть

B1, B2, ..., BR , (4)

C1, C2, ..., CS , (5)

Базисы этих систем соответственно. Тогда rangS1 = R и rangS2 = S. Докажем, что R = S.

По определению базиса каждый вектор системы S1 линейная комбинация векторов системы (4). Так как система (4) базис системы S1 , то каждый вектор системы (4) содержится в S1 и поэтому есть линейная комбинация векторов системы S1 . Поэтому (4) ~ S1. Аналогично доказывается, что (5) ~ S2. Так как S1 ~ S2, то по теореме 2 (4) ~ (5).

Отсюда каждый вектор системы (4) линейная комбинация векторов системы (5), а по определению базиса система (4) линейно независима. Тогда по основной теореме о двух системах векторов R £ S. Аналогично доказавается, что S £ R. Из этих двух неравенств следует R = S.

Теорема доказана.

< Предыдущая		Следующая >