56. Прямые на плоскости. Уравнение линии на плоскости. Основные задачи аналитической геометрии на плоскости

Определение 1. Пусть F(X,Y) - функция от двух действительных переменных X, Y и на плоскости задана аффинная система координат . Уравнение

F(X,Y) = 0 (1)

Называется Уравнением линии L в данной системе координат, если выполняются два условия:

1) координаты X,Y любой точки M(X,Y) € L удовлетворяют уравнению (1);

2) если координаты X,Y точки M(X,Y) удовлетворяют уравнению (1), то точка M(X,Y) € L.

Таким образом, M(X,Y)€ L тогда и только тогда, когда F(X,Y)= 0.

Пусть

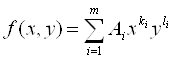(2)

- многочлен. Степенью ненулевого одночлена называется сумма показателей его степеней неизвестных Ki + Li . Степенью многочлена называется наибольшая степень его ненулевых членов. Степень многочлена обозначаем символом deg(F).

Например, степень многочлена равна четырем.

Определение 2. Если F(X,Y) многочлен степени N, и уравнение (1) является уравнением линии L, то линия L называется линией N - го Порядка (в данной системе координат).

Теорема 1. Порядок линии L В аффинной системе координат не зависит от выбора аффинной системы координат и таким образом определяется однозначно.

Основными задачами аналитической геометрии в пространстве являются следующие задачи:

1) по определению линии составить ее уравнение в заданной пространственной системе координат;

2) по уравнению линии изучить ее свойства, установить вид линии и изобразить ее.

Определение 2. Окружностью с центром в точке C радиуса R называется геометрическое место всех точек плоскости, для каждой из которых расстояние до точки C равно R.

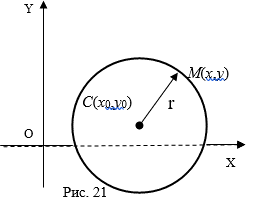
Обозначим окружность с центром в точке C радиуса символом S(C,R).

Выведем уравнение окружности в данной прямоугольной системе координат Oxy. Пусть C(X0,Y0). По определению окружности точка M(X,Y) принадлежит окружности с центром в точке C радиуса R тогда и только тогда, когда

|CM| = R. (5)

По формуле расстояния между двумя точками равенство (5) можно представить в виде:

.

Возведем в квадрат обе части полученного уравнения и находим уравнение окружности:

, (6)

Которое равносильное первоначальному.

Если центр окружности совпадает с началом координат, то уравнение (6) принимает вид:

. (7)

Если в уравнении (6) раскрыть скобки, то его можно представить в виде:

, (8)

Где A = - X0, B = - Y0, С = X02 + Y02 - R2 . Последнее равенство доказывает первую часть теоремы.

Теорема 2. Окружность является линией второго порядка в прямоугольной системе координат, уравнение которой можно представить в виде (8). Обратно, если A2 + B2 - C > 0, то уравнение (8) определяет окружность с центром в точке (-A, -B) радиуса .

Доказательство. Для доказательства второй части теоремы выделим в правой части формулы (9) полные квадраты и представим уравнение (8) в виде

(.

Последнее уравнение является уравнение окружности только тогда, когда A2 + B2 - C > 0. 

Замечание 1. В полярной системе координат, начало которой совпадает с центром окружности, уравнение окружности радиуса R0 задается уравнением

R = R0.

Полярная координата J не входят явно в уравнение окружности: J €[0, 2p), Q €[-p/2, p/2]. Тогда по формулам перехода от полярной системы координат к прямоугольной системе координат получаем Параметрические уравнения окружности:

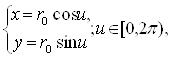. (9)

Упражнение 1. Проверить, что любая точка M(X,Y), координаты которой находятся по формулам (9), удовлетворяют уравнению сферы .

С помощью систем уравнений и неравенств могут быть в пространстве определены различные пространственные тела.

Определение 3. Кругом с центром в точке C радиуса R называется геометрическое место всех точек плоскости, для каждой из которых расстояние до точки C не больше R.

Упражнение 2. Докажите, что круг с центром в точке C(X0,Y0) радиуса R Задается неравенством

.

< Предыдущая		Следующая >