110. Билинейные и квадратичные формы
Рекомендуемая литература
25. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.
26. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. 1997.
27. Воеводин В. В. Линейная алгебра.. М.: Наука 1980.
28. Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А. В., Демидовича Б. П.. М.: Наука, 1981.
29. Бутузов В. Ф., Крутицкая Н. Ч., Шишкин А. А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.
[1, с. 263-272, 346-349], [2, 191-177] , [3,с.291-325] , [4, с.140-147] , [6, с.122-132, 372-380]
3. Билинейная форма и ее свойства. Пусть V - N-мерное векторное пространство над полем P.
Определение 1. Билинейной формой, определенной на V, называется такое отображение G: V2 ® P, которое каждой упорядоченной паре (X, Y) векторов X, Y из ставит в V соответствие число из поля P, обозначаемое G(X, Y), и линейное по каждой из переменных X, Y, т. е. обладающее свойствами:
1) ("X, Y, Z €V) g(X + Y, Z) = G(X, Z) + G(Y, Z);
2) ("X, Y €V) (" A €P) g(aX, Y) = aG(X, Y);
3) ("X, Y, Z €V) g(X, Y + Z) = G(X, Y) + G(X, Z);
4) ("X, Y €V) (" A €P) g(X, aY) = aG(X, Y).
Пример 1. Любое скалярное произведение, определенное на векторном пространстве V является билинейной формой.
2. Функция H(X, Y) = 2X1 Y1- X2 Y2 + X2Y1 , где X = (X1, X2), Y= (Y1, Y2)€R2, билинейная форма на R2.
Определение 2. Пусть V = (V1, V2,…, VN) - базис векторного пространства V. Матрицей билинейной формы G(X, Y) Относительно базиса V называется матрица B = (Bij)N´N, элементы которой вычисляются по формуле Bij = G(VI, VJ):
 .
.
Пример 3. Матрица билинейной формы H(X, Y) (см. пример 2) относительно базиса E1= (1,0), E2 = (0,1) равна ![]() .
.
Теорема 1. Пусть X, Y- координатные столбцы соответственно векторов X, Y в базисе V, B - матрица билинейной формы G(X, Y) Относительно базиса V. Тогда билинейную форму можно записать в виде
G(X, Y)=XtBY. (1)
Доказательство. По свойствам билинейной формы получаем

Пример 3. Билинейной формы H(X, Y) (см. пример 2) можно записать в виде H(X, Y)=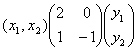 .
.
Теорема 2. Пусть V = (V1, V2,…, VN), U = (U1, U2,…, UN) - Два базиса векторного пространства V, T- матрица перехода от базиса V к базису U. Пусть B = (Bij)N´N И С = (СIj)N´N - Матрицы билинейной формы G(X, Y) Соответственно относительно базисов V и U. Тогда
С = TtBT. (2)
Доказательство. По определению матрицы перехода и матрицы билинейной формы находим:

Определение 2. Билинейная форма G(X, Y) называется Симметричной, если G(X, Y) = G(Y, X) для любых X, Y €V.
Теорема 3. Билинейная форма G(X, Y)- Симметричной тогда и только тогда, когда матрица билинейной формы относительно любого базиса симметричная.
Доказательство. Пусть V = (V1, V2,…, VN) - базис векторного пространства V, B = (Bij)N´N - матрицы билинейной формы G(X, Y) относительно базиса V. Пусть билинейная форма G(X, Y)- симметричная. Тогда по определению 2 для любых I, J = 1, 2,…, N имеем Bij = G(VI, VJ) = G(VJ, VI) = Bji. Тогда матрица B - симметричная.
Обратно, пусть матрица B - симметричная. Тогда B T = B и для любых векторов X = X1V1+ …+ XnVN = VX, Y = Y1V1+ Y2V2+…+ YnVN = VY €V , согласно формуле (1), получаем (учитываем, что число - матрица порядка 1, и при транспонировании не меняется)
G(X, Y) = g(X, Y)T = (XtBY)T = YtB tX = G(Y, X).
| < Предыдущая | Следующая > |
|---|