11. Правило Крамера

Рассмотрим систему N Линейных уравнений с N неизвестными:

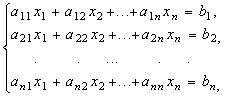(20)

У которой определитель матрицы системы (Определитель системы) не равен нулю, т. е.

Такую систему называем системой линейных уравнений крамеровсого типа. Далее через , будем обозначать определитель, полученный из D заменой I-го столбца столбцом свободных членов:

Разлагая определитель , по элементам I-го столбца, представим его в виде:

(21)

Где , алгебраические дополнения элементов определителя D.

Теорема 10 (Теорема Крамера). Система линейных уравнений крамеровского типа имеет единственное решение, которое находится по формулам:

. (22)

Способ нахождения решений системы N линейных уравнений с N неизвестными и ненулевым определителем называется Правилом Крамера, а формулы называются Формулами Крамера.

Доказательство. Сначала допустим, что решение системы (20), и покажем, что оно находится по формулам (22). В силу определения системы справедливы верные числовые равенства:

Умножив первое из этих равенств на ,второе на , и т. д. N-е на

И сложив почленно получим равенство:

.

По теореме 6 коэффициент равен D , по следствию теоремы 6 все коэффициенты у ,..., равны нулю, правая часть равенства по формуле (21) равна и равенство принимает вид:

.

Аналогично получаем равенства:

Так как , то отсюда находим, что

,

Т. е. решения находятся по формулам (22).

Покажем, что числа, найденные по формулам (22), удовлетворяют уравнениям системы (20). Имеем

.

Эта сумма равна , так как по теореме 6 коэффициент у Равен d, по следствию теоремы 6 коэффициенты у ,..., равны нулю и числа (22) удовлетворяют уравнениям (22). Аналогично устанавливается, что числа (22) удовлетворяют остальным уравнениям системы (20).

Теорема доказана.

Следствие 1. Если система систему n линейных уравнений с n неизвестными не имеет решений или имеет бесконечно много решений, то ее определитель равен нулю.

Действительно, если бы ее определитель был отличен от нуля, то по теореме 9 она бы имела бы единственное решение. Получили противоречие.

Следствие 2. Если система систему n линейных однородных уравнений n неизвестными имеет ненулевое решение, то ее определитель равен нулю.

Действительно, если бы ее определитель был не равен нулю, то по теореме 9 она имела бы единственной нулевое решение. Получили противоречие.

Пример 9. Решить систему

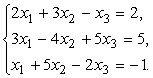
Составим и вычислим определитель системы:

Так как он не равен, то вычислим определители :

.

Отсюда по формулам Крамера находим:

.

Решение системы (2,-1,-1).

< Предыдущая		Следующая >