104. Построение ортонормированного базиса из собственных векторов самосопряженного оператора
1) Составить характеристическое уравнение линейного оператора |A - l.E| = 0.
2) Найдем все корни характеристического уравнения.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A - l.E)X=0.
4) Ортонормируем, полученный базис.
Пример. Линейный оператор A, действующий в евклидовом пространстве Е3, имеет в ортонормированном базисе E1, E2, E3 матрицу
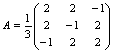 .
.
Найти в Е3 ортонормированный базис из собственных векторов оператора A и составить матрицу оператора A в этом базисе.
Решение. 1) Составить характеристическое уравнение линейного оператора |A - l.E| = 0.

2) Найдем все корни характеристического уравнения: l1=-1, l2 = l3 = 1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид
![]() .
.
3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A - l.E)X=0.
Пусть l1=-1. Матричное уравнение (A - l1E)X=0 принимает вид:

Решая систему, находим решение X = C(1,-2,1), C€R.
Пусть l2 = l3 = 1. Матричное уравнение (A - l1E)X=0 принимает вид:

Решая систему, находим решение X = C1(2,1,0) + C2(-1,0,1), C€R.
4) Ортонормируем, полученный базис.
A1 = (1,-2,1), A2 = (2,1,0), A3 =(-1,0,1).
B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2, ![]() , b3 =(-1/5, 2/5, 1/5).
, b3 =(-1/5, 2/5, 1/5).
 .
.
| < Предыдущая | Следующая > |
|---|