10. Вычисление определителей
Определители 2-го и 3-го порядков можно вычислять по правилу Сарюса. Вычисление определителей порядка большего трем сводится к вычислению определителей меньших порядков разложением определителя по строке или по столбцу. Обычно разлагают по тем строкам (столбцам), в которых имеется много нулей. Для получения нулей используются свойства определителей в частности свойство 8.
Пример 8. Вычислить определитель

![]() .
.
При переходе от первого определителя к второму прибавили к 1-й и к 3-й строкам 2-ю, умноженную на -2, к 4-й - 2-ю, умноженную на -3. Затем разложили определитель по первому столбцу. При переходе от третьего определителя к четвертому прибавили к 2-й строке 1-ю, умноженную на -1, к 3-й - 1-ю, умноженную на -3. Затем разложили определитель по третьему столбцу.
Определители некоторых матриц можно вычислить в общем случае. Например, определители треугольных матриц.
Определение 13. Треугольными матрицами разываются матрицы, у которых все элементы, расположенные по одну сторону от главной диагонали равны нулю, т. о. треугольными матрицами являются следующие матрицы:
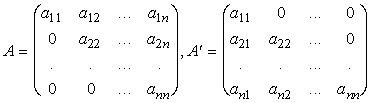 .
.
Теорема 9. Определитель треугольной матрицы равен произведению элементов главной диагонали, т. е.![]() .
.
Доказательство. Доказываем методом математической индукции по N. При N=1,2 утверждение теоремы справедливо. Предположим, что теорема справедлива для N-1 и докажем ее для N. Разлагая ![]() По первому столбцу, получим:
По первому столбцу, получим:
 .
.
Последний определитель по индуктивному предположению равен ![]() . Поэтому
. Поэтому ![]() . Аналогично доказывается и второе равенство. Теорема доказана.
. Аналогично доказывается и второе равенство. Теорема доказана.
| < Предыдущая | Следующая > |
|---|