03. Ступенчатая матрица
Определение 6. Матрицей размерности ![]() называется прямоугольная таблица
называется прямоугольная таблица

Содержащая Mn чисел, расположенных в M строк и n столбцов, числа ![]() называются Элементами матрицы. Если
называются Элементами матрицы. Если ![]() , то матрица называется квадратной матрицей порядка M . Если все элементы матрицы равны нулю, то матрица называется Нулевой матрицей. Элементы AIi называются элементами Главной диагонали.
, то матрица называется квадратной матрицей порядка M . Если все элементы матрицы равны нулю, то матрица называется Нулевой матрицей. Элементы AIi называются элементами Главной диагонали.
Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также Трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют Треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).
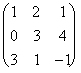 ,
, 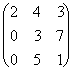 ,
, 
![]() ,
, 
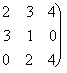 ,
, 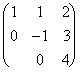 .
.
Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число ![]() ;
;
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство. Доказательство проводим методом математической индукции по числу M строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих M-1 строку и докажем его для матриц, в которых содержится M строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер K , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
 .
.
Можем считать, что элемент ![]() , в противном случае строки матрицы можно переставить. Прибавим ко второй строке матрицы первую, умноженную на число
, в противном случае строки матрицы можно переставить. Прибавим ко второй строке матрицы первую, умноженную на число ![]() , к третьей - первую, умноженную на
, к третьей - первую, умноженную на ![]() и т. д. , к M-й - первую, умноженную на
и т. д. , к M-й - первую, умноженную на ![]() . После этих преобразований матрица примет вид:
. После этих преобразований матрица примет вид:
 . (9)
. (9)
Рассмотрим матрицу, состоящую из последних M-1 строк матрицы (9):
 . 10)
. 10)
Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида:  ,
,
Где элементы ![]()
![]() и
и ![]() не равны нулю. Тогда соответствующими преобразованиями строк матрица (9) преобразуется в матрицу ступенчатого вида:
не равны нулю. Тогда соответствующими преобразованиями строк матрица (9) преобразуется в матрицу ступенчатого вида:
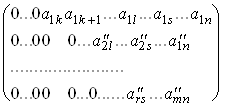 ; (11)
; (11)
Элементы ![]() ,
, ![]() ,...,
,..., ![]() не равны нулю. Теорема доказана.
не равны нулю. Теорема доказана.
| < Предыдущая | Следующая > |
|---|