01. Системы линейных уравнений

Литература

1. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.

2. Ермаков В. И. Общий курс высшей математики. М.: Инфра - М, 2000. с. 5-22

3. Кремер Н. Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.

1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

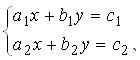
Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений - Метод последовательного Исключения неизвестных или метод Гаусса По имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).

Определение 1. Системой m линейных уравнений с n неизвестными

X1 , x2,..., xn называется система уравнений

(1)

Где A11 ,A12 ,...,Amn - фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые Коэффициентами при Неизвестных, B1 ,B2 ,...,BM - фиксированные числа, называемые свободными Членами.

Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется Однородной.

Определение 2. Решением системы линейных уравнений (1) называется такой упорядоченный набор N чиселПри подстановке которыхВ каждое из уравнений системы вместо соответственно неизвестных X1 , x2 ,..., xn каждое из уравнений системы превращается в истинное числовое равенство.

Система называется Совместной, если она имеет хотя бы одно решение, и называется Несовместной, если она не имеет решений. Совместная система называется Определенной, если она имеет одно решение, и называется Неопределенной, если она не имеет решений.

Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 - множества их решений соответственно.

Определение 3. Говорят, что система линейных уравнений S2 Следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т. е. . Обозначаем .

Определение 4. Говорят, что системы S1 и S2 Равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т. е. . Обозначаем .