6.7.2. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
При большом числе испытаний одно и то же значение X может встретиться nx раз, одно и то ж значение У может встретиться ny раз и одна и та же пара чисел (x; у) может встретиться nxy раз,
причем обычно— объем выборки.
Поэтому данные наблюдений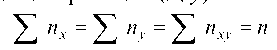
Группируют, т. е. подсчитывают nx, ny, nxy. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.
Если обе линии регрессии У на X и X на У — прямые, то корреляция является линейной.
Выборочное уравнение прямой линии регрессии У на X имеет вид:
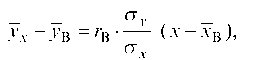
Параметры pyx и В, которые определяются методом наименьших квадратов, имеют вид:
где yx — условная средняя; XВ и Ув — выборочные средние признаков X и У; —x и —у — выборочные средние квадратические отклонения; гВ — выборочный коэффициент корреляции.
Выборочное уравнение прямой линии регресии X на У имеет вид:
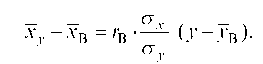
Считаем, что данные наблюдений над признаками X и У заданы в виде корреляционной таблицы с равноотстоящими вариантами.
Тогда переходим к условным вариантам:
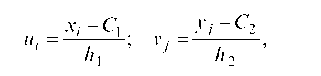
где С1 — варианта признака X, имеющая наибольшую частоту; С 2 — варианта признака У, имеющая наибольшую частоту; h1 — шаг (разность между двумя соседними вариантами X); h2 — шаг (разность между двумя соседними вариантами У).
Тогда выборочный коэффициент корреляции
Величины u, v, su, sv могут быть найдены методом произведений, либо непосредственно по формулам
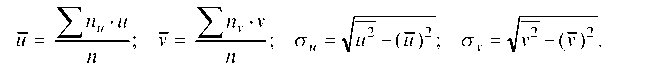
Зная эти величины, найдем параметры, входящие в уравнения регрессии, по формулам
12.1.1. В ящике находятся 6 одинаковых пар перчаток черного цвета и 4 одинаковых пары перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.
Решение. Рассмотрим событие А — две извлеченные наудачу перчатки образуют пару; и гипотезы: B1 — извлечена пара перчаток черного цвета, B2 — извлечена пара перчаток бежевого цвета, B3 — извлеченные перчатки пару не образуют.
Вероятность гипотезы B1 по теореме умножения равна произведению вероятностей того, что первая перчатка черного цвета и вторая перчатка черного цвета, т. е.
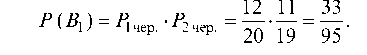
Аналогично, вероятность гипотезы Bi равна:
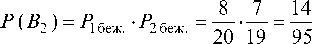
Так как гипотезы B1, B2 и B3 составляют полную группу событий, то вероятность гипотезы B3 равна:
По формуле полной вероятности имеем:
где Pb (A) есть вероятность того, что пару образуют две черные перчатки и Pb1 (A) = 1; pB1 (A) — вероятность того, что пару образуют две бежевые перчатки и Pb2 (A) = 1; и, наконец, РВз( A) — вероятность того, что пару образуют перчатки разного цвета и
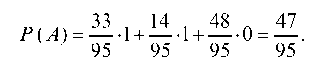
Таким образом, вероятность того, что две наудачу извлеченные перчатки образуют пару равна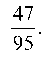
12.1.2. В урне находятся 3 шара белого цвета и 5 шаров черного цвета. Наудачу по одному извлекают 3 шара и после каждого извлечения возвращают обратно в урну. Найти вероятность того, что среди извлеченных шаров окажется:
а) ровно два белых шара, б) не мене двух белых шаров.
Решение. Имеем схему с возвращением, т. е. каждый раз состав шаров не изменяется:
а) при извлечении трех шаров два из них должны быть белыми, а один черный. При этом черный может оказаться или первым, или вторым, или третьим. Применяя совместно теоремы сложения и умножения вероятностей, имеем:
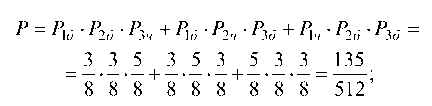
б) вынуть не менее двух белых шаров означает, что белых шаров должно быть или два, или три:
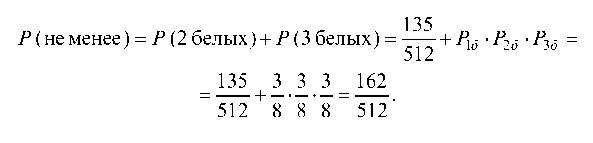
12.1.3. В урне находятся 6 белых и 5 черных шаров. Три шара наудачу последовательно извлекаются без возвращения их в урну. Найти вероятность, что третий по счету шар окажется белым.
Решение. Если третий по счету шар должен быть белым, то первые два шара могут быть белыми, или белым и черным, или черным и белым, или черными, т. е. имеются четыре группы не-
совместных событий. Применяя к ним теорему умножения вероятностей, получим:
P = P1(5 • P2(5 • P3(5 + (P1(5 • Р2ч • P3(5 + P14 • P2(5 • P3(5 ) + Р1ч • Р2ч • P3(5 =
= A A 4 A A 5 A A 5 A A 6=540 = A
= П • 10 • 9 + И • 10 • 9 + И • 10 • 9 + И • 10 • 9 = 990 = IT
| < Предыдущая | Следующая > |
|---|
