7.2.2. Межотраслевой баланс
7.2.2.1. Модель межотраслевого баланса
Балансовый метод применяется для анализа, нормирования, прогноза и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом.
Центральная идея межотраслевого баланса (МОБ) заключается в том, что каждая отрасль в нем рассматривается и как производитель, и как потребитель. Модель МОБ — одна из самых простых экономико-математических моделей. Она представляет собой единую взаимосвязанную систему информации о взаимных поставках продукции между всеми отраслями производства, а также об объеме и отраслевой структуре основных производственных фондов, обеспеченности народного хозяйства ресурсами труда и т. д.
Такая модель позволяет рассчитать сбалансированный план на основе точного учета всех межотраслевых связей и рассмот-
реть при этом множество возможных вариантов. В основе исследований балансовых моделей лежат балансовые таблицы, содержащие данные о производстве и потреблении продукции различных отраслей или предприятий. Характерные черты и особенности этого метода описываются с помощью матричных моделей баланса. Из математических методов здесь главным образом используется аппарат линейной алгебры.
Рассмотрим пример предельно упрощенной системы, состоящей из двух производственных отраслей. Пусть исполнение баланса за предшествующий период характеризуется данными, приведенными в табл. 7.15.
Таблица 7.15
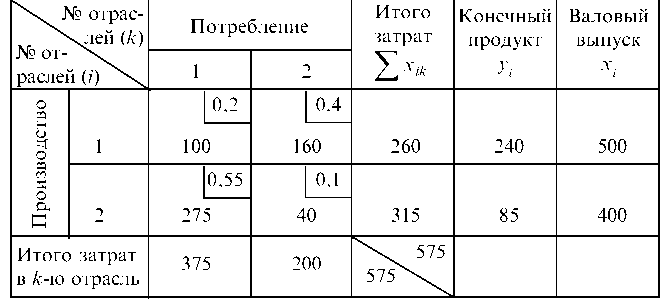
Продукция каждой отрасли частично идет на внешнее потребление (конечный продукт), а частично используется в качестве сырья, полуфабрикатов или других средств производства в других отраслях, в том числе и в данной. Эту часть продукции называют производственным потреблением. Поэтому каждая из рассматриваемых отраслей выступает и как производитель продукции (1-й столбец продукции) и как ее потребитель (1-я строка таблицы). Приведенную таблицу конкретного примера можно записать и в более общем виде (табл. 7.16).
Обозначим через хг валовый выпуск продукции г-й отрасли за планируемый период и через у — конечный продукт, идущий на внешнее для рассматриваемой системы потребление (средства производства других экономических систем, потребление населения, образование запасов и т. д.). Таким образом, разность (хг - ^г) составляет часть продукции i-й отрасли, предназначенную для внутрипроизводственного потребления. Предполагаем, что баланс составляется в стоимостном разрезе. Обозначим через xik часть продукции i-й отрасли, которая потребляется k-й отраслью, для обеспечения выпуска ее продукции в размере xi.
Таблица 7.16
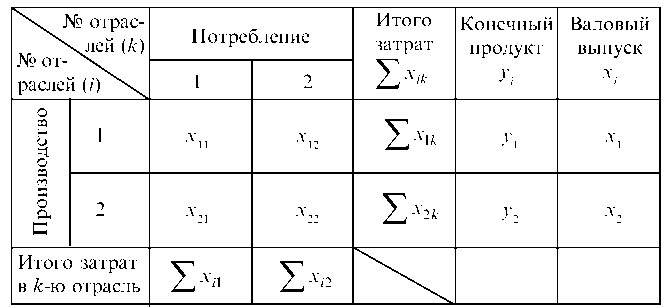
Очевидно, величины, расположенные в строках, связаны следующими балансовыми равенствами:
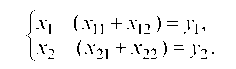
Отсюда стоимостной баланс в общем виде запишется уравнениями:
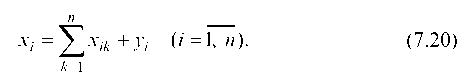
Рассмотрев отношение количества продукции i-й отрасли, поступающей в k-ю отрасль для обеспечения выпуска ее продукции в размере xk, получим затраты на единицу валовой продукции

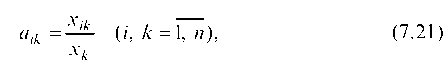
откуда
Рассчитываем агк по формуле (7.21) и записываем в табл. 7.15 в углах соответствующих клеток.
Найденные коэффициенты прямых затрат и образуют неотрицательную матрицу прямых затрат:
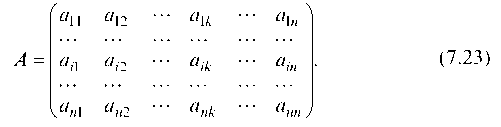
(7.23)
Подставляя в уравнение (7.20) соотношения (7.22) получим:
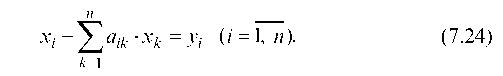
(7.24)
Систему уравнений МОБ (7.24) запишем в матричной форме

(Е - А) X = Г, (7.25)
где Е — единичная матрица, А — матрица прямых затрат (7.23), X и Г — столбцовые матрицы
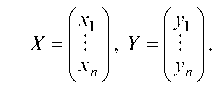
7.2.2.2. Полные внутрипроизводственные затраты
Пусть матрица
Р = (Е - А)-1, Р = || Р1к ||, (7.26)
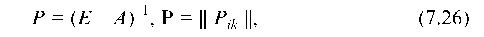
тогда из (7.25): (Е - А)-1 ¦ (Е - А) ¦ X = (Е - А)-1 ¦ Г и, так как
(Е - А) ¦ (Е - А) = Е и ЕХ = X, то получаем, что объемы произ-
водства отраслей X определяются как
X = РГ

(7.27)
по заданным величинам конечного продукта потребления Г и матрице Р, которую называют матрицей коэффициентов полных затрат.
Элементы матрицы Р включают не только затраты i-й продукции, необходимой для создания одной единицы k-й продукции, но и те затраты, которые необходимы для создания в каждой отрасли одной единицы конечного продукта.
Значит полные затраты Pik включают как прямые aik так и косвенные (Pik - aik) затраты. Очевидно, что всегда Pik > aik, точнее
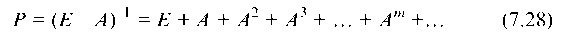
Матрицы А2, А3, ... , Ат,... называются матрицами коэффициентов косвенных затрат 1-го, 2-го и т. д. порядков и коэффициенты полных затрат получают в виде суммы коэффициентов прямых затрат и косвенных затрат.
Прямые затраты не отражают в полной мере сложных количественных взаимосвязей, наблюдающихся в народном хозяйстве. Они в частности не отражают обратных связей, имеющих далеко не маловажное значение.
Как возникают косвенные затраты? Например, на изготовление трактора в виде прямых затрат расходуется чугун, сталь, и т. д., но для производства стали также нужен чугун. Таким образом, кроме прямых затрат чугуна, имеются и косвенные затраты чугуна, связанные с производством трактора. В эти косвенные затраты входит и чугун, необходимый для создания того количества чугуна, которое составляет прямые затраты. Эти косвенные затраты могут иногда существенно превышать прямые затраты.
Исходя из (7.27), валовый выпуск k-й отрасли хк определяется как
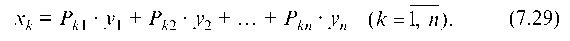
Модель межотраслевого баланса (7.24), (7.25) или (7.29) позволяет решить следующие задачи:
1) определить объем конечной продукции отраслей y1, y2, ., yn по заданным объемам валовой продукции х1, х2, ..., хп;
2) по заданной матрице коэффициентов прямых затрат А определить матрицу коэффициентов полных затрат P, элементы которой служат важными показателями для планирования развития отраслей;
3) определить объем валовой продукции отраслей хь х2, ., хп по заданным объемам конечной продукции у1, у2, ..., уп.
4) по п заданным объемам конечной или валовой продукции отраслей х1, .у2, х3, .у4, ... определить оставшиеся п объемов.
7.2.2.4. Решение типовой задачи
Рассмотрим пример составления межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы, заданной матрицей коэффициентов прямых затрат А и вектором конечной продукции Г:
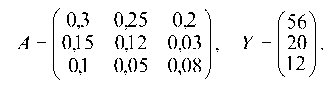
Найти коэффициенты полных затрат: плановые объемы валовой продукции X = (х1; х2, Х3); величину межотраслевых потоков, т. е. значения хгк (г = 1, 2, 3; к = 1, 2, 3); матрицу косвенных затрат; по заданному вектору увеличения косвенного выпуска продукции ДГ определить изменение плана ДХ.
Находим матрицу (Е - А):
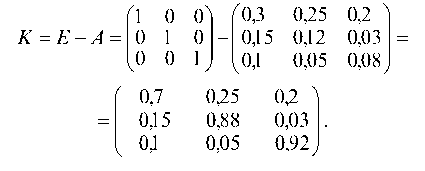
Для определения матрицы полных затрат (7.28) обращаем матрицу К.
Первый способ нахождения К 1 = (Е - А)-1. Вычисляем определитель
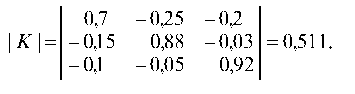
Так как | К | ф 0, то существует матрица К 1 = Р обратная заданной матрице К.
Находим алгебраические дополнения для элементов матрицы К.
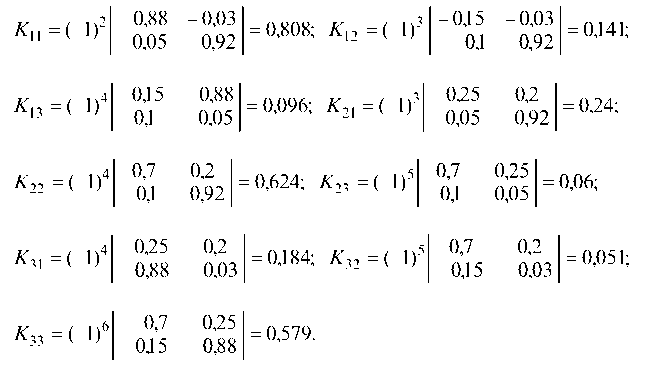
Из алгебраических дополнений составляем транспонированную матрицу и, деля ее на | К |, получаем обратную матрицу К -1:
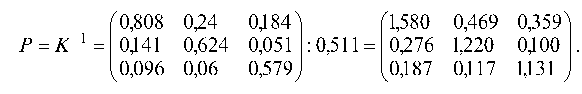
Рассмотрим другой способ нахождения обратной матрицы К 1 с помощью жордановых исключений. Составляем табл. 7.17.
Таблица 7.17

Совершаем последовательно три шага жордановых исключений, меняя местами Ьг - и х., получаем табл. 7.18—7.20.
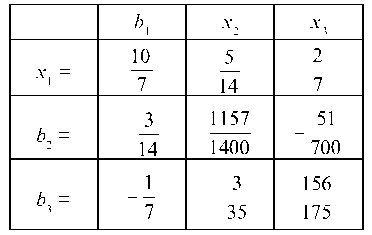
Таблица 7.19
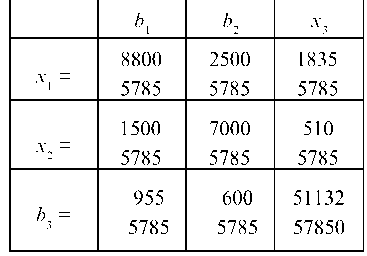
Таблица 7.20
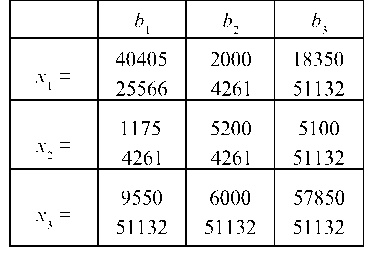
Внутри табл. 7.20 стоит обратная матрица K 1. Округляя до третьего знака после запятой, имеем:
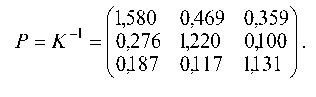
| (1,580 0,469 0,359^ | ( 56 ^ | (102,197^ | ||
| X = PY = | 0,276 1,220 0,100 | 20 | = | 41,047 |
| 0Д87 0,117 1Д31 0 | I12 0 | 26,383 |
Следовательно, плановые объемы валовой продукции трех отраслей, необходимые для обеспечения заданного уровня конечной продукции равны:
х1 = 102,2; х2 = 41,0; х3 = 26,4.
Для составления баланса рассчитываем межотраслевые потоки средств производства по формуле (7.22):
x11 = 0,3 • 102,2 = 37,7; x21 = 0,15 • 102,2 = 15,3; x31 = 0,1 • 102,2 = 10,2; x12 = 0,25 • 41,0 = 10,2; x22 = 0,12 • 41,0 = 4,9; x32 = 0,05 • 41,0 = 2,1; x13 = 0,2 • 26,4 = 5,3; x23 = 0,03 • 26,4 = 0,8; x33 = 0,08 • 26,4 = 2,1.
Результаты вычислений представим в форме межотраслевого баланса (табл. 7.21). Величина чистой продукции определяется здесь как разница между валовой продукцией отрасли и суммой межотраслевых потоков в каждом столбце.
Таблица 7.21
| ^^^Потребляющие отрасли Произво-^^^^ дящие отрасли^^ | 1 | 2 | 3 | Конечная
продукция | Валовая
продукция |
| 1 | 30,7 | 10,2 | 5,3 | 56 | 102,2 |
| 2 | 15,3 | 4,9 | 0,8 | 20 | 41,0 |
| 3 | 10,2 | 2,1 | 2,1 | 12 | 26,4 |
| Чистая продукция | 46,0 | 23,8 | 18,2 | - | - |
| Валовая продукция | 102,2 | 41,0 | 26,4 | - | 169,6 |
На основе заданных матриц Y и A по уровню конечного продукта и коэффициентов прямых затрат получен полностью сбалансированный план общего производства продукции и ее рас-
пределения как между отраслями в качестве средств производства, так и для конечного использования.
Матрицу косвенных затрат найдем из формулы (7.28):
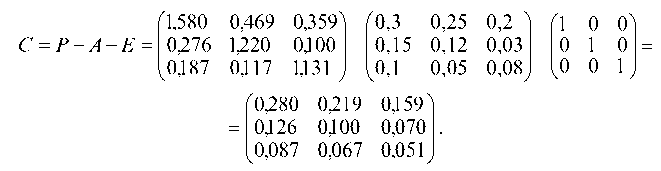
Определяем изменение плана ДХ, которое потребуется при увеличении конечного выпуска продукции 1-й отрасли на 20, 2-й — на 10 и 3-й — на 5 (единиц).
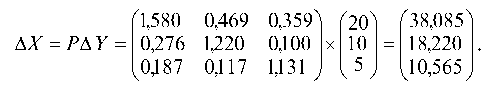
Следовательно, потребуется увеличить валовый выпуск 1-й отрасли на Дх1 = 38,1, 2-й отрасли на Дх2 = 18,2 и 3-й отрасли на 10,6 (единиц).
| < Предыдущая | Следующая > |
|---|