7.1.1. Задача оптимального производства продукции

Для изготовления двух видов изделий I и II используются три вида сырья.

На производство единицы изделия I требуется затратить сырья первого вида 13 кг, сырья второго вида — 32 кг, сырья третьего вида — 58 кг.

На производство единицы изделия II требуется затратить сырья первого вида 24 кг, сырья второго вида — 32 кг и сырья третьего вида — 29 кг.

Производство обеспечено сырьем первого вида в количестве 312 кг, сырьем второго вида — 480 кг, сырьем третьего вида — 696 кг.

Прибыль от реализации единицы готового изделия I составляет 4 усл. ед., а изделия II — 3 усл. ед.

Требуется составить план производства изделий I и II, обеспечивающий максимальную прибыль от их реализации, если заранее планируется изготовление не менее 10 единиц изделий I и II.

Решение. Рассмотрим математическую модель задачи. Если за *1 взять количество изделий I, планируемых к выпуску, а за.¾ — количество изделий II, то получим задачу линейного программирования.

найти максимум линейной функции

Геометрическое решение задачи

Поскольку задача двухмерная, то ее можно решить графически. Система ограничений (7.1) дает многоугольник решений. Для его построения проводим прямые, являющиеся границами многоугольника и с помощью пробной точки, например (0; 0), определим полуплоскости, задаваемые этими прямыми (рис. 86):

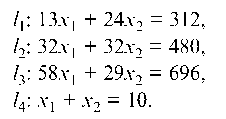
В пересечении соответствующих полуплоскостей получим шестиугольник ABCDEF'.

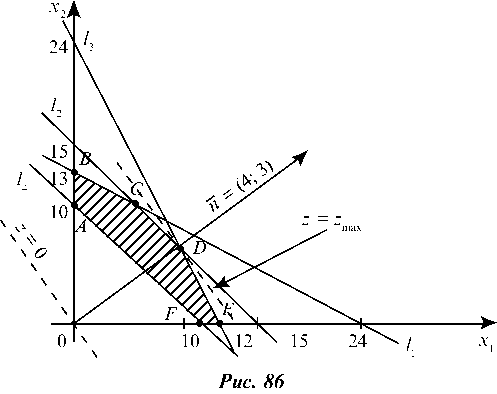
Для нахождения max z построим из начала координат вектор п = (4; 3) и перпендикулярную ему линию уровня z = 0, т. е. прямую 4X1 + 3X2 = 0.

Далее передвигаем линию уровня z = const в направлении возрастания z, т. е. параллельно самой себе в направлении вектора п. В последней пересекаемой вершине D получаем наибольшее значение z. Вершина D — это точка пересечения прямых /2 и /3. Находим координаты точки D из системы:

Решая систему, найдем, что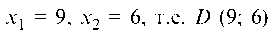И при

этом(усл. ед.).

Для решения задачи симплекс — методом приведем систему ограничений (7.1) к форме равенств с помощью неотрицательных дополнительных переменных

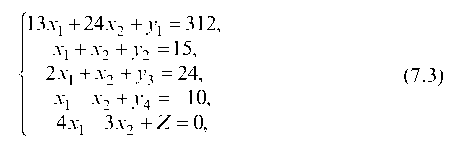
при этом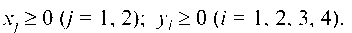

Записываем систему с помощью укороченных таблиц (табл. 7.1).

Так как в I — столбце есть отрицательный элемент, то его нужно сделать положительным. Выбираем у 4 — строку с отрицательным свободным членом «-10».

В этой же строке есть отрицательные элементы, выбираем какой-нибудь из них, например, «-1» в *1 — столбце. И *1 — столбец принимаем в качестве разрешающего столбца.

Делим свободные члены на соответствующие элементы разрешающего столбца, получаем {24, 15, 12, 10} и наименьшее положительное отношение будет соответствовать разрешающей строке, следовательно, у4 — строка является разрешающей, а элемент 1-1 I разрешающим элементом. Совершаем шаг модифицирован-ногожорданова исключения (ШМЖИ) с разрешающим элементом -1 по правилу:

1) на месте разрешающего элемента стоит величина ему обратная;

2) элементы разрешающей строки делятся на разрешающий элемент;

3) элементы разрешающего столбца делятся на разрешающий элемент и знак меняется;

4) остальные элементы новой таблицы находятся по формуле прямоугольника [17, стр. 521:

Получаем табл. 7.2, при этом переменные *1 и у4 меняются местами. Из таблицы видно, что свободные коэффициенты в I — столбце не отрицательны, следовательно, получено опорное решение: X1 = 10, X2 = 0, у1 = 182, у2 = 5, у3 = 4, у4 = 0, Z = 40. Геометрически это означает, что мы находимся в вершине F (10;0) многоугольника решений ABCDEF'.

Это решение не является оптимальным, так как в Z — строке имеется отрицательный коэффициент, улучшаем план.

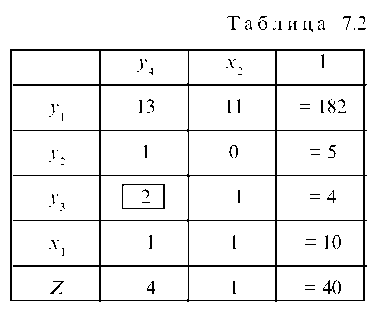
Выбираем разрешающий элемент по правилу: выбираем столбец с наименьшим отрицательным элементом в z-строке — разрешающий столбец, делим свободные члены в I-столбце на соответствующие коэффициенты и наименьшее положительное отношение соответствует разрешающей строке. На пересечении стоит разрешающий элемент [~2] . Совершая ШМЖИ с разрешающим элементом 2 по выше приведенному правилу, получаем табл. 7.3.

Решение, получаемое из табл. 7.3, также не является опти-

и-

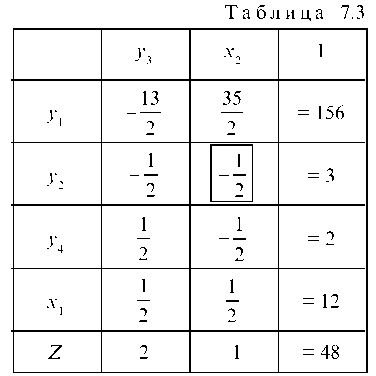
мальным, так как в Z-строке имеется отрицательный коэф' циент. Определяя из табл. 7.3 разрешающий элемент

и

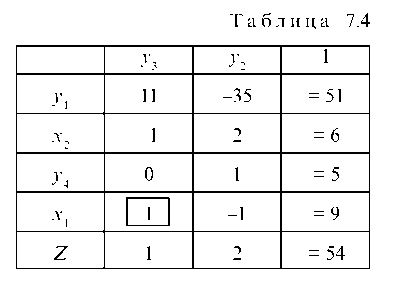
совершая ШМЖИ, приходим к табл. 7.4, в которой все коэффициенты в Z-строке неотрицательны, а, следовательно, max Z уже достигнут и ему соответствует решение X1 = 9, X2 = 6, при этом

Zmax = 54 (усл. ед.).

Ответ: максимальная прибыль Z = 54 (усл. ед.) достигается при изготовлении 9 единиц изделий I и 6 единиц изделий II.

< Предыдущая		Следующая >