Вариант № 10

Задача 1 Коллинеарны ли векторы и , построенные по векторам и ?

Рассм.

Рассм. , след. векторы и коллинеарны

Задача 2 Найти косинус угла между векторами и .

Рассм. векторы и ;

, откуда ;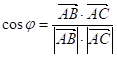

Вычислим ;

;

.

Задача 3 Вычислить площадь параллелограмма, построенного на векторах и .

.

; рассм.

;

.

Задача 4 Компланарны ли векторы ?

.

;

Рассм. 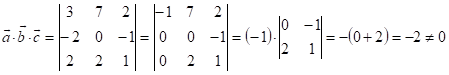, след. векторы Не компланарны.

Задача 5 Найти расстояние от точки до плоскости, проходящей через точки : .

Составим уравнение плоскости , проходящей через точки :

Рассм. векторы ;

Выберем норм. вектор плоскости ;

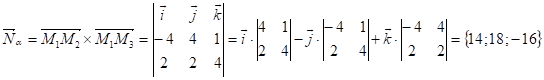Рассм. ; составим уравнение плоскости :

;

Определим теперь искомое расстояние от точки до плоскости по формуле:

.

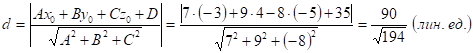Задача 6 Написать уравнение плоскости, проходящей через точку перпендикулярно

вектору : .

Рассм. вектор ; рассм. произв. т. и рассм. вектор , т. е.

.

Задача 7 Найти угол между плоскостями .

Рассм. норм. векторы ; искомый угол между плоскостями

и равен углу между их норм. векторами ; определим угол из условия:

;

Вычислим ;

;

.

Задача 8 Написать канонические уравнения прямой, заданной как линия пересечения

плоскостей .

;

;

;

Выберем напр. вектор ;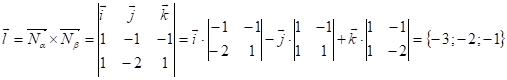

Выберем произв. т. ; положим , а координаты определим из системы уравнений: ;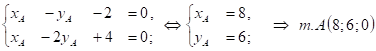

Запишем канонические ур-я прямой : .

Задача 9 Найти точку пересечения прямой и плоскости :

; ;

Запишем параметрические ур-я прямой

Определим координаты т. Пересечения пр. и пл. :

;

.

Задача 10 Найти точку , симметричную точке относительно

Прямой .

Рассм. плоскость , проходящую через точку перпендикулярно

Прямой ; выберем и запишем ур-е пл-ти :

;

Запишем параметр. ур-я прямой :

Определим координаты т. Пересечения пр. и пл. :

;

;

Определим координаты искомой точки из условия, что т. есть середина отрезка :

;

;

;

.

< Предыдущая Следующая >