Вариант № 19

Вывести уравнение теплопроводности для тонкого ограниченного стержня, боковая поверхность которого теплоизолирована: сформулировать возможные типы краевых условий.

Определить температуру в произвольной точке х стержня в произвольный момент времени t - функцию u(x, t) в общем виде, при заданных краевых условиях, если начальные условия заданы функцией u(x,0) = f(x); решить задачу для заданной функции f(x); определить приближенно температуру стержня в точке xo в момент времени to (мин.), взяв три первых ненулевых члена ряда Фурье.

Типы краевых условий:

А) концы стержня теплоизолированы, т. е. ,

Б) левый конец стержня теплоизолирован, а правый поддерживается при нулевой

температуре, т. е.

В) правый конец стержня теплоизолирован, а левый поддерживается при нулевой

температуре, т. е., .

Коэффициент а2 температуропроводности: медь - 11.2 ∙ 10-5;

Сталь - 1.27 ∙ 10-5;

алюминий - 8.80 ∙ 10-5.

Условия задачи

F(x) = ,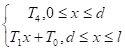

Тип краевых условий – а

Материал – медь

Xo = , to = 40

Решение

1.  Ищем решение уравнения теплопроводности с начальным условием: u(x,0) = f(x) =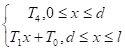

и граничными условиями:

в виде u(x, t) = X(x)T(t).

Подставляем его в исходное уравнение X(x)T′(t) = а2 X″(x)T(t).

Отсюда

Следовательно: Граничные условия

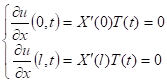
Получили задачу Штурма – Лиувилля для X(x):

.

Решение ищем в виде:

Характеристическое уравнение

1)  - кратный корень.

Общее решение имеет вид:

Граничные условия: 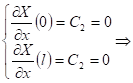при

2) 

Общее решение имеет вид:

Граничные условия: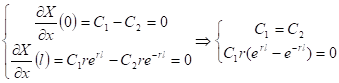

Т. к. - тривиальное решение.

3) 

Общее решение имеет вид:

Граничные условия: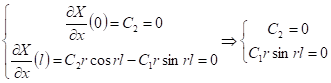

Если

Пусть С1=1, тогда , при .

Этим же значениям соответствуют решения уравнения , имеющие вид:

Частное решение уравнения теплопроводности:

; , где Со=const

;

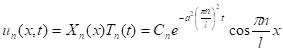
Общее решение имеет вид:

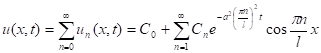
Начальные условия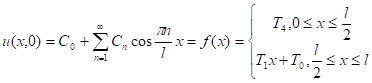

Разлагаем f(x) в ряд Фурье по косинусам

Сравнивая ряды, видим:

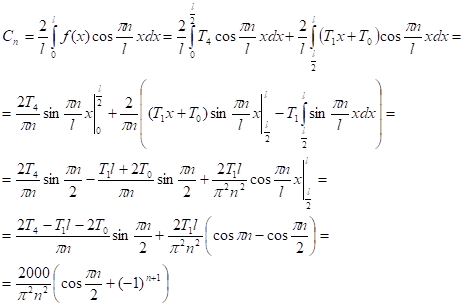
Общее решение представится в виде:

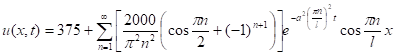
Приближённое значение температуры стержня в точке xo = в момент времени to = 40:

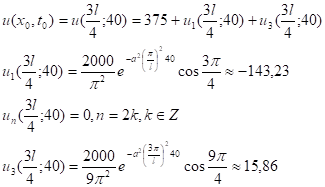
< Предыдущая		Следующая >