Вариант № 01

Вариант 1

Задача 1.Вычислить.

;

Решение.

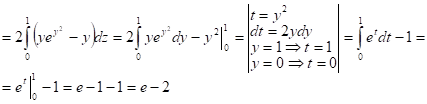
Задача 2.Вычислить.

;

Решение.

Область ограничена поверхностью И плоскостями

.

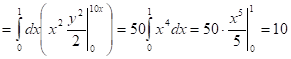Задача 3. Найти объём тела, заданного ограничивающими его поверхностями

.

Решение.

Первое уравнение задает цилиндрическую

Поверхность с образующими, параллельными

Оси .

Два последних уравнения определяют

Гиперболические параболоиды.

Проекция тела на плоскость

Ограничена параболой И прямой .

Точки пересечения параболы и прямой находим:

Следовательно, проекция тела на плоскость

Определяется неравенствами

Объем тела равен:

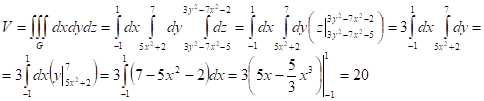
Задача 4. Тело задано ограничивающими его поверхностями, - плотность. Найти массу тела.

.

Решение:

Введём цилиндрические координаты: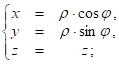

Поверхности можно записать в цилиндрических координатах:

Тогда тело : ,

Масса тела

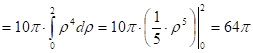
Задача 5. Найти объём тела, заданного неравенствами

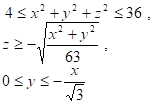
Решение:

Введём сферические координаты:

В сферических координатах неравенства принимают вид:

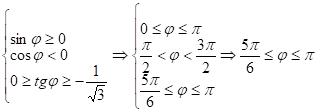
Объем тела равен:

Следующая >