Вариант № 22
1. Найти область определения функции и изобразить её на плоскости: ![]() .
.
 Для заданной функции область определяется следующими неравенствами:
Для заданной функции область определяется следующими неравенствами: ![]() ,
, ![]() ,
, ![]() . Из первого неравенства получаем:
. Из первого неравенства получаем: ![]() , или
, или ![]() , или
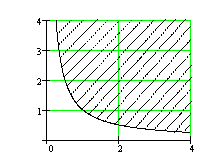
, или ![]() . Таким образом, областью определения данной функции является множество точек, расположенных в первой четверти координатной плоскости выше линии гиперболы
. Таким образом, областью определения данной функции является множество точек, расположенных в первой четверти координатной плоскости выше линии гиперболы ![]() . Сама линия гиперболы и оси координат в область определения функции не входят (см. рисунок). Ответ:
. Сама линия гиперболы и оси координат в область определения функции не входят (см. рисунок). Ответ: ![]()
![]() и
и ![]() , и
, и ![]() .
.
2. Вычислить частные производные ![]() и
и ![]() сложной функции в данной точке:
сложной функции в данной точке: ![]() при
при ![]() .
.
Частные производные сложной функции двух переменных ![]() находятся по формулам
находятся по формулам ![]() и
и ![]() . В данном случае
. В данном случае ![]() . Следовательно,
. Следовательно, ![]() ,
,
![]() . Заметим, что в точке
. Заметим, что в точке ![]() промежуточные переменные равны:
промежуточные переменные равны: ![]() . Подставляя в частные производные
. Подставляя в частные производные ![]() , получим:
, получим: ![]() ,
,  . Ответ:
. Ответ: ![]() ,
,  .
.
3. Найти уравнение касательной плоскости и нормали к указанной поверхности в данной на ней точке: ![]() .
.
Касательная плоскость и нормаль к поверхности ![]() в точке
в точке ![]() имеют следующие уравнения: а)
имеют следующие уравнения: а)  (касательная плоскость):
(касательная плоскость):  (нормаль). В данном случае
(нормаль). В данном случае ![]() . Найдём частные производные от
. Найдём частные производные от ![]() в точке
в точке ![]() :
: 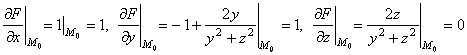 . Подставим найденные частные производные в уравнения касательной плоскости и нормали:
. Подставим найденные частные производные в уравнения касательной плоскости и нормали: ![]() ,
, ![]() . Или
. Или ![]() ,
, ![]() . Ответ: а) Уравнение касательной плоскости:
. Ответ: а) Уравнение касательной плоскости: ![]() ; б) Уравнение нормали:
; б) Уравнение нормали: ![]() .
.
4. Найти наибольшее и наименьшее значения функции ![]() в области D:
в области D: ![]() .
.
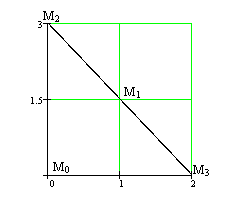 Составим уравнение стороны BC треугольника ΔOBC:
Составим уравнение стороны BC треугольника ΔOBC: ![]() . Найдём стационарные точки в области D:
. Найдём стационарные точки в области D: ![]() . Решая систему
. Решая систему ![]() , получим стационарную точку
, получим стационарную точку ![]() . Значение функции в этой точке равно
. Значение функции в этой точке равно ![]() . На границе области D
. На границе области D ![]() функция имеет вид
функция имеет вид ![]() - точек экстремума нет. На границе области D
- точек экстремума нет. На границе области D ![]() функция имеет вид
функция имеет вид ![]() - точек экстремума нет. На границе области D
- точек экстремума нет. На границе области D ![]() функция имеет вид
функция имеет вид ![]() . Тогда
. Тогда ![]() , следовательно, точка
, следовательно, точка ![]() является стационарной точкой на прямой
является стационарной точкой на прямой ![]() , причём
, причём ![]() . Находим значение функции в угловых точках области D:
. Находим значение функции в угловых точках области D: ![]() . Сравнивая все значения
. Сравнивая все значения ![]() , видим, что наибольшее значение
, видим, что наибольшее значение ![]() функция принимает в точке
функция принимает в точке ![]() , а наименьшее значение
, а наименьшее значение ![]() - на сторонах треугольника
- на сторонах треугольника ![]() и
и ![]() . Ответ: наибольшее значение функции
. Ответ: наибольшее значение функции ![]() в точке
в точке ![]() , наименьшее значение
, наименьшее значение ![]() - на сторонах треугольника
- на сторонах треугольника ![]() и
и ![]() .
.
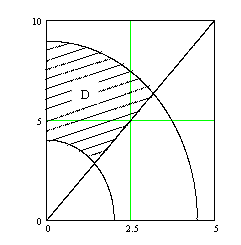
5. Изменить порядок интегрирования:  .
.
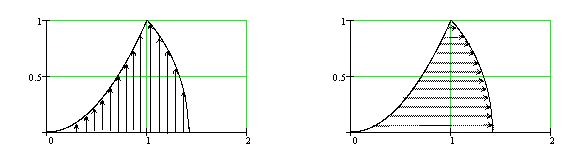 |
Восстановим область интегрирования (D) по пределам повторных интегралов:
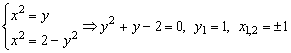 .
.
Порядок интегрирования в данном интеграле показан штриховкой на первом графике. На втором графике штриховка изменена на вертикальную. Из рисунка видим, что данная область является X – трапецией. На левой границе ![]() , на правой границе
, на правой границе ![]() . Поэтому
. Поэтому ![]() и в результате подстановки пределов получим следующий повторный интеграл:
и в результате подстановки пределов получим следующий повторный интеграл: 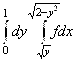 . Ответ:
. Ответ: 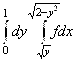 .
.
6. 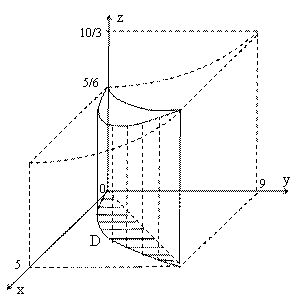 Найти объём тела, ограниченного указанными поверхностями:
Найти объём тела, ограниченного указанными поверхностями: ![]() . Основанием тела в плоскости ХОУ является область D, ограниченная параболой
. Основанием тела в плоскости ХОУ является область D, ограниченная параболой ![]() и прямой
и прямой ![]() . Снизу тело ограничено плоскостью
. Снизу тело ограничено плоскостью ![]() , сверху – поверхностью
, сверху – поверхностью ![]() (см. рисунок). Таким образом,
(см. рисунок). Таким образом,
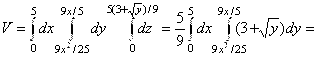
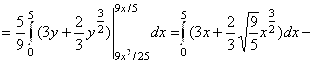
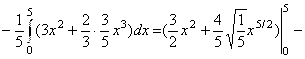
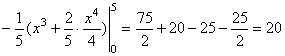 .
.
Ответ: ![]() .
.
7. Найти объём тела, ограниченного указанными поверхностями: ![]() .
.
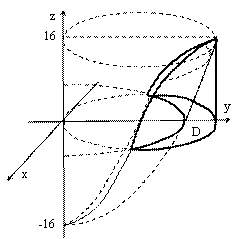 Преобразуем уравнения цилиндрической поверхности:
Преобразуем уравнения цилиндрической поверхности: ![]() . Сверху тело ограничено поверхностью параболоида вращения
. Сверху тело ограничено поверхностью параболоида вращения ![]() , а снизу – координатной плоскостью
, а снизу – координатной плоскостью ![]() (см. рисунок). Удобно перейти к цилиндрическим координатам:
(см. рисунок). Удобно перейти к цилиндрическим координатам: ![]() . Уравнением окружности будет
. Уравнением окружности будет ![]() , уравнением параболоида будет
, уравнением параболоида будет ![]() . При
. При ![]() найдём точки пересечения окружностей
найдём точки пересечения окружностей ![]() и
и ![]() , получаем:
, получаем: ![]() . Область интегрирования будет область
. Область интегрирования будет область ![]() . Следовательно,
. Следовательно, 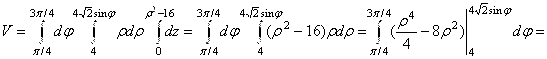
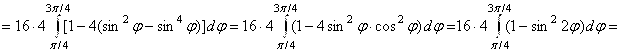
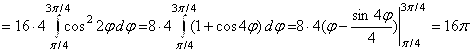 . Ответ:
. Ответ: ![]() .
.
8. Найти объём тела, ограниченного указанными поверхностями: ![]() .
.
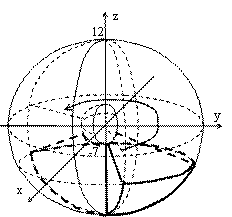 Тело расположено между двумя концентрическими сферами с центрами в начале координат радиуса 7 и 12, конусом (снизу), и двумя плоскостями
Тело расположено между двумя концентрическими сферами с центрами в начале координат радиуса 7 и 12, конусом (снизу), и двумя плоскостями ![]() и
и ![]() . Перейдём к сферической системе координат:
. Перейдём к сферической системе координат: ![]() . Якобиан преобразования равен
. Якобиан преобразования равен ![]() . Уравнение малой сферы будет
. Уравнение малой сферы будет ![]() , большой сферы -
, большой сферы - ![]() , На плоскости
, На плоскости ![]() будет
будет ![]() или
или ![]() , а на плоскости
, а на плоскости ![]() будет
будет ![]() или
или ![]() . Уравнение конуса переходит в уравнение
. Уравнение конуса переходит в уравнение ![]() . Таким образом, тело занимает следующую область:
. Таким образом, тело занимает следующую область: ![]() . Объём тела равен:
. Объём тела равен: ![]() . Или
. Или 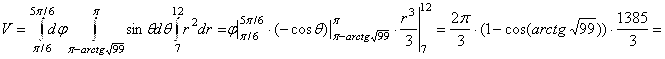
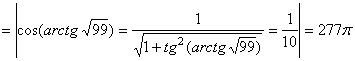 . Ответ:
. Ответ: ![]() .
.
9.  Найти массу пластинки:
Найти массу пластинки: ![]()
Пластинка занимает область D, изображённую на рисунке. Область неудобна для интегрирования в декартовой системе координат. Поэтому перейдём к эллиптической системе координат: ![]() . Уравнением меньшего эллипса будет:
. Уравнением меньшего эллипса будет: ![]() . Аналогично, для большего эллипса получим:
. Аналогично, для большего эллипса получим: ![]() . Якобиан преобразования равен
. Якобиан преобразования равен ![]() . На прямой линии
. На прямой линии ![]() имеем
имеем ![]() . Область, занимаемая пластинкой, есть
. Область, занимаемая пластинкой, есть ![]() . Тогда
. Тогда 
![]() . Ответ:
. Ответ: ![]() .
.
10. Найти массу тела: ![]() .
.
 Тело представляет часть шара, «вырезанную» цилиндрической поверхностью
Тело представляет часть шара, «вырезанную» цилиндрической поверхностью ![]() Цилиндр пересекается с поверхностью сферы
Цилиндр пересекается с поверхностью сферы ![]() на высоте
на высоте ![]() (см. рисунок). Область интегрирования:
(см. рисунок). Область интегрирования: ![]()
![]() . Интегрирование в декартовой системе координат неудобно. Перейдём к цилиндрической системе координат:
. Интегрирование в декартовой системе координат неудобно. Перейдём к цилиндрической системе координат: ![]() . Таким образом, тело занимает следующую область:
. Таким образом, тело занимает следующую область: ![]() . При этом плотность тела равна
. При этом плотность тела равна ![]() . Масса тела равна:
. Масса тела равна: ![]() . Или
. Или  . Ответ:
. Ответ: ![]() .
.
11. Вычислить криволинейный интеграл по формуле Грина: ![]() Контур ΔABC, где A(0; 0), B(1; 0), C(1; 1).
Контур ΔABC, где A(0; 0), B(1; 0), C(1; 1).
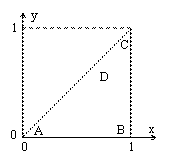 Преобразуем криволинейный интеграл по замкнутому контуру в двойной по формуле Грина:
Преобразуем криволинейный интеграл по замкнутому контуру в двойной по формуле Грина: ![]() . Область интегрирования изображена на рисунке. Для заданного интеграла получаем:
. Область интегрирования изображена на рисунке. Для заданного интеграла получаем: ![]() . Уравнением прямой AC будет
. Уравнением прямой AC будет ![]() . Тогда
. Тогда 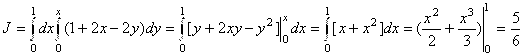 .
.
Ответ: ![]() (Ошибка в условии задачи).
(Ошибка в условии задачи).
12. Вычислить массу дуги кривой (L) при заданной плотности ![]() :
:
![]() .
.
 Массу дуги вычисляем с помощью криволинейного интеграла первого рода:
Массу дуги вычисляем с помощью криволинейного интеграла первого рода: ![]() . В данном примере линия и плотность заданы в декартовых координатах, где
. В данном примере линия и плотность заданы в декартовых координатах, где ![]() . Следовательно,
. Следовательно, 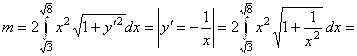
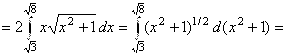
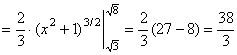 . Ответ:
. Ответ: ![]() .
.
13. Вычислить работу силы ![]() при перемещении вдоль линии
при перемещении вдоль линии ![]() от точки M к точке N:
от точки M к точке N: 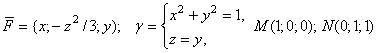 .
.
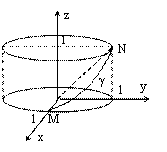 Работу вычисляем по формуле:
Работу вычисляем по формуле: ![]() . Линия
. Линия ![]() находится в пересечении цилиндрической поверхности
находится в пересечении цилиндрической поверхности ![]() и плоскости
и плоскости ![]() (см. рисунок). Перейдём к параметрическому заданию линии:
(см. рисунок). Перейдём к параметрическому заданию линии: ![]() . Найдём значение параметра T, при котором достигаются точки M и N;
. Найдём значение параметра T, при котором достигаются точки M и N; ![]() ;
; ![]() . Тогда
. Тогда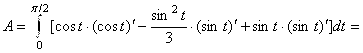
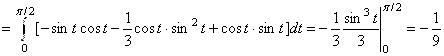 .
.
Ответ: Работа равна ![]() .
.
14. Найти производную функции ![]() в точке
в точке ![]() по направлению внешней нормали
по направлению внешней нормали ![]() к поверхности
к поверхности ![]() , заданной уравнением
, заданной уравнением ![]() , или по направлению вектора
, или по направлению вектора ![]() :
: ![]() .
.
Производная по направлению находится по формуле:  , где
, где ![]() - координаты единичного вектора данного направления. Найдём частные производные функции
- координаты единичного вектора данного направления. Найдём частные производные функции ![]() в заданной точке:
в заданной точке:  . Следовательно,
. Следовательно, ![]() . Найдём единичный вектор заданного направления
. Найдём единичный вектор заданного направления ![]() :
: 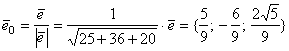 . Тогда производная по заданному направлению равна:
. Тогда производная по заданному направлению равна: ![]() . Ответ:
. Ответ: ![]() .
.
15. Найти наибольшую скорость изменения скалярного поля ![]() в заданной точке М:
в заданной точке М: ![]() .
.
Наибольшую скорость характеризует градиент поля: ![]() .
.
Вычислим координаты градиента: ![]() ,
, ![]() ,
, ![]() . Таким образом,
. Таким образом, ![]() .
.
Величина скорости есть модуль градиента: ![]() .
.
Ответ: Наибольшая скорость изменения поля в заданной точке равна ![]() .
.
16. Вычислить расходимость и вихрь в произвольной точке М, а также найти уравнения векторных линий поля градиента скалярного поля ![]() :
: ![]() .
.
По заданному скалярному полю ![]() построим поле его градиентов:
построим поле его градиентов: ![]() . Дивергенция (расходимость) вектора
. Дивергенция (расходимость) вектора ![]() определяется формулой:
определяется формулой: ![]() . Для градиента получаем:
. Для градиента получаем: ![]() . Ротор вектора
. Ротор вектора ![]() вычисляется как символический определитель третьего порядка:
вычисляется как символический определитель третьего порядка:
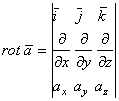 . Для поля градиентов :
. Для поля градиентов : 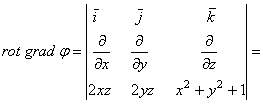
![]() .
.
Уравнение векторных линий поля ![]() определяется системой дифференциальных уравнений:
определяется системой дифференциальных уравнений: ![]() . Для заданного поля
. Для заданного поля ![]() :
:
![]() . Из первого равенства
. Из первого равенства ![]() следует
следует ![]() или
или ![]() . Из равенства
. Из равенства ![]() исключим Y. Получим
исключим Y. Получим 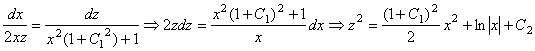 . Итак, уравнения векторных линий поля градиентов задаётся как семейство кривых от пересечения следующих поверхностей:
. Итак, уравнения векторных линий поля градиентов задаётся как семейство кривых от пересечения следующих поверхностей: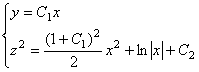 . Ответ:
. Ответ: ![]() ,
, ![]() , урвнения векторных линий поля градиентов:
, урвнения векторных линий поля градиентов: 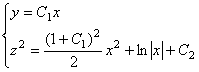 .
.
17. Найти поток векторного поля ![]() через часть плоскости Р, расположенную в 1-ом октанте (нормаль образует острый угол с осью OZ):
через часть плоскости Р, расположенную в 1-ом октанте (нормаль образует острый угол с осью OZ): ![]() .
.
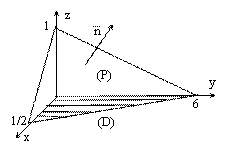 Запишем уравнение плоскости в отрезках:
Запишем уравнение плоскости в отрезках: ![]() или
или ![]() и изобразим её на чертеже (см. рис.). Найдём нормальный вектор:
и изобразим её на чертеже (см. рис.). Найдём нормальный вектор: ![]() . Нормируем нормальный вектор:
. Нормируем нормальный вектор: ![]() . Поток векторного поля находится по формуле
. Поток векторного поля находится по формуле ![]() , где
, где ![]() - проекция вектора поля
- проекция вектора поля ![]() на нормаль к поверхности:
на нормаль к поверхности: ![]() . Поверхностный интеграл сведём к двойному интегралу по области D, являющейся проекцией Р на координатную плоскость ХОУ:
. Поверхностный интеграл сведём к двойному интегралу по области D, являющейся проекцией Р на координатную плоскость ХОУ: ![]() . При этом
. При этом ![]() . Из уравнения поверхности
. Из уравнения поверхности ![]() . Тогда
. Тогда ![]()
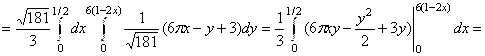
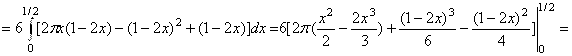
![]() .
.
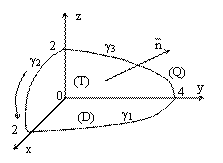
18…19. Тело Т лежит в 1-ом октанте и ограничено плоскостями координат и поверхностью Q, заданной уравнением ![]() . Вычислить:
. Вычислить:
А) поток поля вектора ![]() через поверхность, ограничивающую тело Т (воспользоваться формулой Остроградского);
через поверхность, ограничивающую тело Т (воспользоваться формулой Остроградского);
 В) циркуляцию поля вектора
В) циркуляцию поля вектора ![]() вдоль линии пересечения поверхности Q с плоскостями координат в направлении от точки пересечения Q с осью ОХ к точке пересечения Q с осью OY ( воспользоваться формулой Стокса):
вдоль линии пересечения поверхности Q с плоскостями координат в направлении от точки пересечения Q с осью ОХ к точке пересечения Q с осью OY ( воспользоваться формулой Стокса): ![]() .
.
А) Линии пересечения поверхности с координатными плоскостями.
С плоскостью XOY ![]() ; с плоскостью XOZ
; с плоскостью XOZ ![]() с плоскостью YOZ
с плоскостью YOZ ![]() (см. рисунок, рассматриваются линии только в первом октанте). Поток поля
(см. рисунок, рассматриваются линии только в первом октанте). Поток поля ![]() через поверхность, ограниченную этими линиями находим по формуле Гаусса-Остроградского:
через поверхность, ограниченную этими линиями находим по формуле Гаусса-Остроградского:
![]() . Находим дивергенцию:
. Находим дивергенцию: ![]() . Тогда
. Тогда 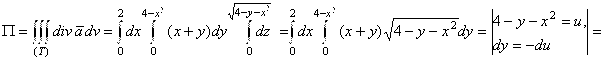
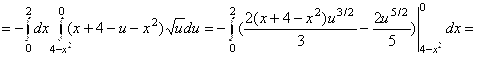
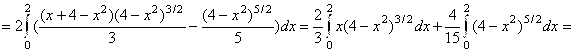
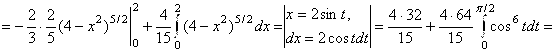

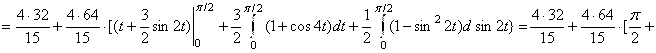
![]() .
.
В) Циркуляцию поля вектора ![]() вдоль линии
вдоль линии ![]() вычислим по формуле Стокса:
вычислим по формуле Стокса: ![]() . Вычислим ротор данного поля:
. Вычислим ротор данного поля:
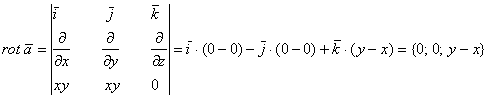 . Найдём вектор
. Найдём вектор ![]() :
: ![]() (это внешняя нормаль). Вычислим скалярное произведение:
(это внешняя нормаль). Вычислим скалярное произведение: ![]() . Таким образом, циркуляция векторного поля равна:
. Таким образом, циркуляция векторного поля равна:

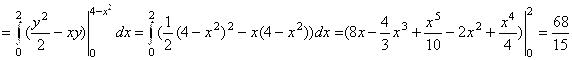 . Ответ:
. Ответ: ![]() .
.
40. Убедиться, что поле вектора ![]() потенциально, найти потенциал поля и вычислить работу при перемещении точки единичной массы из точки А в точку В:
потенциально, найти потенциал поля и вычислить работу при перемещении точки единичной массы из точки А в точку В: ![]() .
.
Вычислим ротор вектора ![]() :
:
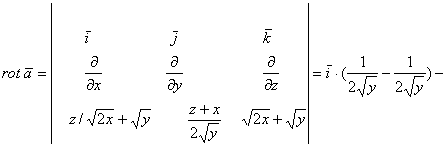
![]() . Следовательно, поле вектора
. Следовательно, поле вектора ![]() является потенциальным. Восстановим потенциал поля:
является потенциальным. Восстановим потенциал поля: 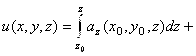
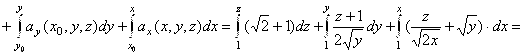
![]()
![]() (за точку M0 взята точка M0(1, 1, 1)). Найдём работу по перемещению точки:
(за точку M0 взята точка M0(1, 1, 1)). Найдём работу по перемещению точки: ![]() .
.
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|