Вариант № 10
Вар.10
Задача 1: Найти область определения функции ![]() . Нарисовать область на координатной плоскости.
. Нарисовать область на координатной плоскости.
Область определения функции ![]() , т. е. границей области определения данной функции будут прямые
, т. е. границей области определения данной функции будут прямые ![]() и
и ![]() .
.
Задача 2: Найти частные производные и полный дифференциал ![]()

Задача 3: Вычислить значения частных производных ![]() функции
функции ![]() в точке
в точке ![]()
![]()
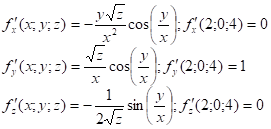
Задача 4: Вычислить значение производной сложной функции ![]() , где
, где ![]() при
при ![]()
![]()
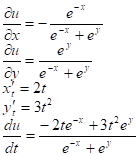
При ![]()
![]()
![]()
Задача 5: Вычислить значения частных производных функции ![]() , заданной неявно, в заданной точке
, заданной неявно, в заданной точке ![]()
![]() или
или ![]()
![]() ;
; ![]()
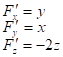
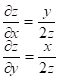 В точке
В точке ![]() :
: 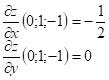
Задача 6: Найти градиент функции ![]() и производную по направлению
и производную по направлению ![]() в точке
в точке![]()
![]() ;
; ![]()

Задача 7: Найти уравнения касательной плоскости и нормали к заданной поверхности ![]() в точке
в точке ![]()
Поверхность задана неявно ![]()
![]() ;
; ![]()
![]()
![]()
![]() ;
; ![]()
Уравнение касательной плоскости: ![]()
![]()
Уравнение нормали: 
Задача 8: Найти вторые частные производные функции ![]() . Убедиться в том, что
. Убедиться в том, что ![]()
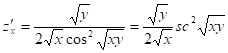 ;
;  ;
;
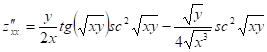 ;
;
![]() ;
;
 ;
;
![]() ;
;
Значит ![]()
![]()
Задача 9: Проверить, удовлетворяет ли функция ![]() уравнению:
уравнению:![]()
![]() ;
;
![]()
![]()
![]()
Подставляем полученные значения производных в исходное уравнение:
![]()
Правая часть уравнения тождественно равна левой части, следовательно,
Функция ![]() удовлетворяет данному уравнению.
удовлетворяет данному уравнению.
Задача 10: Исследовать функцию на экстремум ![]()
![]() ;
; ![]()
![]() Т.
Т.![]() - стационарная точка
- стационарная точка
![]()
![]()
![]()
![]() и
и ![]() т.
т.![]() - точка максимума
- точка максимума
Задача 11: Найти наибольшее и наименьшее значения функции ![]() в области
в области ![]() , ограниченной заданными линиями
, ограниченной заданными линиями ![]()
1) ![]() Т.
Т.![]() - стационарная точка
- стационарная точка
![]() ;
; ![]() ;
; ![]()
![]() В т.
В т.![]() - нет экстремума
- нет экстремума
2) Исследуем значения функции на границах области ![]() :
:
а) сторона АС:![]()
![]() т.
т.![]() - стационарная точка на
- стационарная точка на
стороне АС ![]()
в) сторона АВС: ![]()
![]() на АВС стационарные
на АВС стационарные
точки![]() :
:![]() и
и![]() :
:![]()
Сравнивая все полученные значения, в которых могут достигаться наибольшее и наименьшее значения, видим, что:
![]()
![]() ;
;
![]()
![]()
Задача 12: Найти условный экстремум функции ![]() при
при ![]()
![]()
![]() не обращается в нуль ни в одной точке прямой
не обращается в нуль ни в одной точке прямой ![]()
Составим функцию Лагранжа: ![]()
![]()
![]() ;
; ![]()
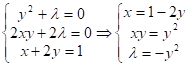
Система имеет 2 решения:
1) ![]() , т. е. т.
, т. е. т.![]()
2) ![]() , т. е. т.
, т. е. т.![]()
Выясним наличие условного экстремума двумя способами:
1) ![]() При условии
При условии ![]()
![]()
В т. ![]()
![]() функция имеет условный минимум в
функция имеет условный минимум в
Т. ![]() и
и ![]()
В т. ![]()
![]() функция имеет условный максимум в
функция имеет условный максимум в
Т. ![]() и
и ![]()
2) Рассмотрим т.![]() . Имеем
. Имеем ![]()
![]() ;
; ![]()
![]() ;
; ![]()
В т. ![]()
![]() .
.
Значит:

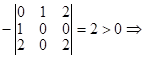 т.
т.![]() - точка условного минимума
- точка условного минимума
Рассмотрим т.![]() . Имеем
. Имеем ![]()
В т. ![]() :
:
![]() ;
; ![]() ;
;
![]() .
.
Значит:
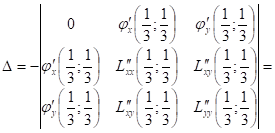
 т.
т.![]() - точка условного максимума
- точка условного максимума
| < Предыдущая | Следующая > |
|---|