Вариант № 22

Вариант 22

Двойные и тройные интегралы

Задача 1. Изменить порядок интегрирования

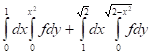
Область интегрирования ограничена

Дугой окружности, параболой

И осью OX.

Выразим переменную из уравнений

И при условии .

Получим и

Область интегрирования D задается системой неравенств

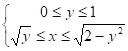
Следовательно, двойной интеграл вычисляется по формуле:

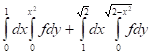
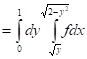
Задача 2. Вычислить:

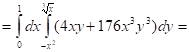
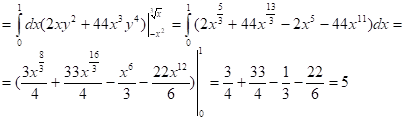
Задача 3. Вычислить:

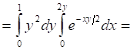
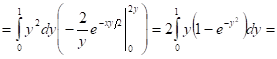
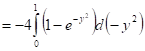
Задача 4. Найти площадь фигуры, ограниченной данными линиями:

Поскольку фигура ограничена дугами окружностей,

Перейдем к полярным координатам:

Уравнения линий принимают вид:

Или

Значит, искомая фигура задается неравенствами:

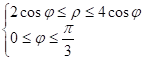
Площадь фигуры:

Задача 5. Найти объём тела, заданного ограничивающими его поверхностями:

.

Решение.

1) Находим уравнение линии

Пересечения поверхности

и плоскости :

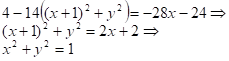
Следовательно, уравнение линии :

- окружность;

2)Перейдём к полярным координатам:

Тогда круг :

Значит:

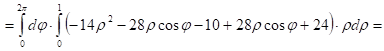
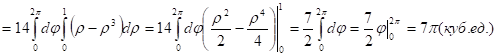
Задача 6. Пластинка D задана неравенствами, Поверхностная плотность Найти массу пластинки.

,

Решение.

Произведем замену переменных

; . Имеем ; ;

; ;

,

Где задается неравенствами:

Перейдем к полярным координатам

Имеем

< Предыдущая		Следующая >