Вариант № 09
В задачах 1-9 найти общие решения уравнений и частные решения, если есть начальные условия.
1. ![]() . Уравнение является однородным. Сделаем замену
. Уравнение является однородным. Сделаем замену ![]() . Тогда
. Тогда ![]() . Получим уравнение
. Получим уравнение ![]() , или
, или
![]() . Запишем уравнение в дифференциалах:
. Запишем уравнение в дифференциалах:
![]() . Разделяем переменные:
. Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение: ![]() или
или ![]() . Получим:
. Получим: ![]() . Вернёмся к переменной Y, делая обратную замену U=Y/X:
. Вернёмся к переменной Y, делая обратную замену U=Y/X: ![]() . Определим постоянную С из начальных условий:
. Определим постоянную С из начальных условий: ![]() , отсюда C=−1. Подставляя это значение в общее решение, получим частное решение:
, отсюда C=−1. Подставляя это значение в общее решение, получим частное решение: ![]() . Ответ:
. Ответ: ![]() .
.
2. ![]() . Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями
. Уравнение является линейным. Решим его методом Бернулли. Будем искать решение в виде произведения Y=U∙V, где U и V неизвестные функции, определяемые в данном случае уравнениями ![]() и
и ![]() или
или ![]() . Решим первое уравнение:
. Решим первое уравнение: ![]() или
или ![]() . Отсюда
. Отсюда ![]() (произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим:
(произвольная постоянная добавляется при решении второго уравнения). Потенцируя, находим: ![]() . Подставим найденную функцию U во второе уравнение и решим его:
. Подставим найденную функцию U во второе уравнение и решим его: ![]() или
или ![]() . Тогда
. Тогда
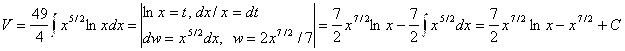 . Таким образом, общее решение имеет вид:
. Таким образом, общее решение имеет вид: ![]() или
или ![]() . Найдём C, исходя из начальных условий:
. Найдём C, исходя из начальных условий: ![]() . Тогда
. Тогда ![]() . Таким образом, частное решение есть
. Таким образом, частное решение есть ![]() . Ответ:
. Ответ: ![]() .
.
3. ![]() . Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение:
. Это уравнение Бернулли. Его можно решать непосредственно как линейное уравнение, применяя метод вариации произвольной постоянной. Решим однородное уравнение: ![]() или
или ![]() . Отсюда находим
. Отсюда находим ![]() . Будем предполагать, что решение исходного уравнения имеет
. Будем предполагать, что решение исходного уравнения имеет
такую же структуру, но C=C(X), т. е. ![]() , где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём
, где C(X) – некоторая неизвестная функция. Определим эту функцию, подставляя данное (предполагаемое) решение в исходное уравнение. Найдём ![]() .
.
Тогда ![]() . Или
. Или ![]() .
.
Разделяем переменные: ![]() . Интегрируем уравнение:
. Интегрируем уравнение:![]() . Следовательно,
. Следовательно, ![]() . Общие решение уравнения
. Общие решение уравнения ![]() или
или ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() , т. е. C1=−5. Тогда частным решением будет
, т. е. C1=−5. Тогда частным решением будет ![]() . Ответ:
. Ответ: ![]() .
.
4. ![]() .
.
Найдём частные производные: ![]() ,
,
![]() . Следовательно, уравнение является уравнением в полных дифференциалах. Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что
. Следовательно, уравнение является уравнением в полных дифференциалах. Левая часть этого уравнения представляет полный дифференциал некоторой функции U(X,Y), так что ![]() и
и ![]() . Проинтегрируем первое уравнение по X:
. Проинтегрируем первое уравнение по X: ![]() . Таким образом,
. Таким образом, ![]() , где φ(Y) – произвольная функция. Найдём эту функцию, пользуясь вторым уравнением. С одной стороны
, где φ(Y) – произвольная функция. Найдём эту функцию, пользуясь вторым уравнением. С одной стороны ![]() . С другой стороны,
. С другой стороны, ![]() . Приравнивая эти выражения, получим:
. Приравнивая эти выражения, получим: ![]() . Отсюда,
. Отсюда, ![]() . Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае
. Согласно уравнению, DU=0. Решением уравнения будет U(x, y)=C. В данном случае ![]() . Ответ:
. Ответ: ![]() .
.
5. ![]() Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует искомая функция Y. Сделаем замену
Уравнение второго порядка, допускающее понижение порядка. В уравнении отсутствует искомая функция Y. Сделаем замену ![]() . Тогда
. Тогда ![]() . Получим однородное уравнение первого порядка:
. Получим однородное уравнение первого порядка: ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Или
. Или ![]() . Интегрируем уравнение:
. Интегрируем уравнение:
![]() . Или:
. Или:
![]() . Определим постоянную C1, пользуясь начальным
. Определим постоянную C1, пользуясь начальным
Условием ![]() :
: ![]() . Следовательно,
. Следовательно, ![]() . Тогда
. Тогда
![]() . Определим C2, пользуясь вторым начальным условием
. Определим C2, пользуясь вторым начальным условием ![]() :
: ![]() . Окончательно,
. Окончательно, ![]() . Ответ:
. Ответ: ![]() .
.
6. ![]() Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения
Линейное неоднородное уравнение второго порядка. Решим уравнение методом вариации произвольных постоянных. Найдём сначала решение однородного уравнения ![]() . Характеристическое уравнение
. Характеристическое уравнение ![]() имеет два корня:
имеет два корня: ![]() . Получаем два частных решений:
. Получаем два частных решений: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х:
. Будем считать, что решение неоднородного уравнения имеет такую же структуру, но С1 и С2 являются функциями переменной Х: ![]() . Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений:
. Тогда, в соответствии с методом вариации произвольных постоянных, неизвестные функции С1(Х) и С2(Х) определяются системой уравнений: 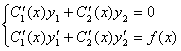 , где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему:
, где F(X) – правая часть неоднородного уравнения. В данном случае имеем систему: 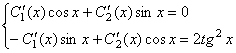 . Решим систему методом Крамера:
. Решим систему методом Крамера: ![]() . Интегрируя, получаем:
. Интегрируя, получаем: ![]()
![]() . Следовательно, решением неоднородного уравнения будет
. Следовательно, решением неоднородного уравнения будет
![]() . Или:
. Или:
![]() . Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С1=С3 и С2=С4. Окончательно,
. Теперь можно вернуться к прежним обозначениям произвольных постоянных. Положим С1=С3 и С2=С4. Окончательно, ![]() .
.
Ответ: ![]() .
.
7. ![]() . Линейное неоднородное уравнение четвёртого порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение четвёртого порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет четыре корня:
имеет четыре корня: ![]() . Получаем четыре частных решения:
. Получаем четыре частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Здесь множитель Х3 обусловлен тем, что корень характеристического уравнения R=0 совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=0). Найдём производные YЧн::
. Здесь множитель Х3 обусловлен тем, что корень характеристического уравнения R=0 совпадает с коэффициентом α в экспоненте EαX, «стоящей» в правой части уравнения (α=0). Найдём производные YЧн:: ![]() ,
, ![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение: ![]() . Отсюда находим
. Отсюда находим ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() .
.
Ответ: ![]() .
.
8. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два равных корня:
имеет два равных корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные YЧн::
. Найдём производные YЧн:: ![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]() . Отсюда находим
. Отсюда находим ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() . Воспользуемся начальными условиями:
. Воспользуемся начальными условиями: ![]() . По первому условию
. По первому условию ![]() . Найдём
. Найдём ![]() . Тогда, по второму условию,
. Тогда, по второму условию, ![]() . Отсюда находим:
. Отсюда находим: ![]() . Частное решение уравнения будет
. Частное решение уравнения будет ![]() . Ответ:
. Ответ: ![]() .
.
9. ![]() . Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения
. Линейное неоднородное уравнение второго порядка. Найдём сначала решение однородного уравнения ![]() Характеристическое уравнение
Характеристическое уравнение ![]() имеет два равных корня:
имеет два равных корня: ![]() . Получаем два частных решения:
. Получаем два частных решения: ![]() . Общее решение однородного уравнения имеет вид:
. Общее решение однородного уравнения имеет вид: ![]() . Найдём частное решение неоднородного уравнения, исходя из структуры его правой части:
. Найдём частное решение неоднородного уравнения, исходя из структуры его правой части: ![]() . Найдём производные yчн::
. Найдём производные yчн::
![]()
![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]()
![]() . Сокращая на
. Сокращая на ![]() и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, находим
и приравнивая коэффициенты при одинаковых функциях в левой и правой частях равенства, находим ![]() . Или
. Или![]() . Следовательно,
. Следовательно, ![]() . Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного:
. Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного: ![]() . Ответ:
. Ответ: ![]() .
.
10. Решить систему линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами ![]() , где
, где  - функции от T, M – матрица коэффициентов, при начальных условиях
- функции от T, M – матрица коэффициентов, при начальных условиях ![]() :
:
 .
.
Запишем систему по исходным данным:
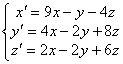 . Ищем решение в виде
. Ищем решение в виде 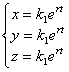 . Тогда
. Тогда 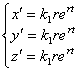 . Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты
. Подставляя это в систему, получим систему алгебраических уравнений, которая определяет неизвестные коэффициенты ![]() :
: 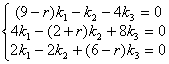 . Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы:
. Приравнивая определитель системы к нулю, получим характеристическое уравнение исходной системы: 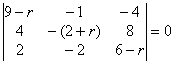 . Раскроим определитель:
. Раскроим определитель: ![]() . Или
. Или ![]() . Следовательно,
. Следовательно, ![]() . При
. При ![]() получим систему:
получим систему: 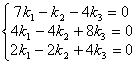 . Отбросим третье уравнение, как линейно зависимое. Получим
. Отбросим третье уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили первое частное решение:
. Получили первое частное решение: ![]() . При
. При ![]() получим систему:
получим систему: 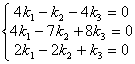 . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили второе частное решение:
. Получили второе частное решение: ![]() .
.
При ![]() получим систему:
получим систему: 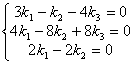 . Отбросим второе уравнение, как линейно зависимое. Получим
. Отбросим второе уравнение, как линейно зависимое. Получим ![]() . Положим
. Положим ![]() . Тогда
. Тогда ![]() . Получили третье частное решение:
. Получили третье частное решение: ![]() . Общее решение записывается как линейная комбинация частных решений:
. Общее решение записывается как линейная комбинация частных решений: 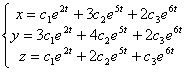 .
.
Найдём произвольные постоянные, пользуясь начальными условиями. При T=0 получим
Систему: 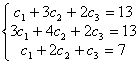 . Исключим С1, складывая первое уравнение с третьим, умноженным на (-1) и второе уравнение с третьим, умноженным на (-3). Получим:
. Исключим С1, складывая первое уравнение с третьим, умноженным на (-1) и второе уравнение с третьим, умноженным на (-3). Получим: 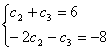 . Следовательно,
. Следовательно, ![]() . Таким образом, частное решение системы следующее:
. Таким образом, частное решение системы следующее: 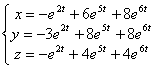 . Ответ:
. Ответ: 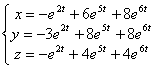 .
.
12. Найдите уравнение кривой, проходящей через точку ![]() и обладающей свойством, что угловой коэффициент касательной в любой точке М(X,Y) кривой вдвое больше углового коэффициента радиус-вектора точки М.
и обладающей свойством, что угловой коэффициент касательной в любой точке М(X,Y) кривой вдвое больше углового коэффициента радиус-вектора точки М.
Угловой коэффициент касательной к кривой ![]() в точке
в точке ![]() равен
равен ![]() . Угловой коэффициент радиус-вектора точки М0 равен
. Угловой коэффициент радиус-вектора точки М0 равен ![]() . Приравняем эти коэффициенты:
. Приравняем эти коэффициенты: ![]() . Это равенство должно выполняться для любой точки кривой. Поэтому введём обычные обозначения:
. Это равенство должно выполняться для любой точки кривой. Поэтому введём обычные обозначения: ![]() . Получим уравнение:
. Получим уравнение: ![]() . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем: ![]() . По условию точка
. По условию точка ![]() находится на прямой, т. е.
находится на прямой, т. е. ![]() . Тогда
. Тогда ![]() . Ответ:
. Ответ: ![]() .
.
13. Закон ускоренного развития науки, сформулированный Энгельсом, гласит: «Наука развивается пропорционально сумме знаний, унаследованных ею от предшествующего поколения». Определите, во сколько раз возрастёт сумма знаний к 2000 году по отношению к 1975 году, если известно, что сумма знаний удваивается каждый год.
Пусть сумма накопленных знаний к моменту времени T равна V(T). Тогда, по условию задачи, ![]() , где K – некоторый коэффициент. Решим уравнение:
, где K – некоторый коэффициент. Решим уравнение: ![]()
![]() Пусть в момент
Пусть в момент ![]() сумма знаний была равна V0. Тогда
сумма знаний была равна V0. Тогда ![]() . Известно что за 10 лет сумма удвоится, т. е.
. Известно что за 10 лет сумма удвоится, т. е. ![]() . Отсюда находим:
. Отсюда находим: ![]() . Тогда
. Тогда ![]() . В 1975 году сумма знаний составляла величину
. В 1975 году сумма знаний составляла величину ![]() , а в 2000 стала равной
, а в 2000 стала равной ![]() . Следовательно,
. Следовательно, 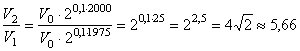 . Ответ: в
. Ответ: в ![]() раза.
раза.
| < Предыдущая | Следующая > |
|---|