Теория вероятности и математическая статистика 04
Контрольные задания
І. Теория вероятностей.
1А. Определение сложных событий.
Задача 1.1 Техническое устройство состоит из двух последовательно и трех параллельно соединенных блоков. Определить сложное событие, характеризующее исправное состояние устройства.
Введем обозначения:
Событие A – блок 1 исправен (последовательно соединён)
Событие B – блок 2 исправен (последовательно соединён)
Событие C – блок 3 исправен (параллельно соединён)
Событие D – блок 4 исправен (параллельно соединён)
Событие E – блок 5 исправен (параллельно соединён)
Событие G - техническое устройство исправно.
Так как параллельному соединению соответствует сумма событий, а последовательному соединению — произведение событий.
Тогда Сложное событие G, характеризующее исправное состояние устройства, можно определить следующим образом:
G=A*B*(С+D+E)
2А. Способы определения вероятностей.
Задача 2.1. Бросаются два игральных кубика и рассматриваются события:
![]() – сумма выпавших очков четная;
– сумма выпавших очков четная;
![]() – произведение выпавших очков менее 37;
– произведение выпавших очков менее 37;
![]() – сумма выпавших очков более 15.
– сумма выпавших очков более 15.
Определить вероятности Р(![]() ), Р(
), Р(![]() ), Р(
), Р(![]() ).
).
На выпавшей грани «первой» игральной кости может появиться одно очко, два очка,…, шесть очков. Аналогичные шесть элементарных исходов возможны и при бросании другой кости. Каждый из исходов бросания «первой» может сочетаться с каждым из исходов бросания «второй». Таким образом общее число возможных элементарных исходов испытания равно ![]() . Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
. Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
Найдём вероятность того, что сумма выпавших очков четная.
Благоприятствующими интересующему нас событию (сумма выпавших очков четная) являются следующие исходы:
1)1, 1 2)1, 3 3)1, 5 4)2, 2 5)2, 4 6)2, 6
7)3, 1 8)3, 3 9)3, 5 10)4, 2 11)4, 4 12)4, 6
13)5, 1 14)5, 3 15)5, 5 16)6, 2 17)6, 4 18)6, 6
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов испытания: ![]()
Найдём вероятность того, что произведение выпавших очков менее 37:
Благоприятствующими интересующему нас событию (произведение выпавших очков менее 37) являются все возможные исходы, так как произведение даже двух наибольших значений меньше 37 (6*6=36<37).
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов испытания: ![]()
Найдём вероятность того, что сумма выпавших очков более 15.
Благоприятствующих интересующему нас событию (сумма выпавших очков более 15) исходов нет, так как сумма даже двух наибольших значений меньше 15 (6+6=12<15).
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов испытания: ![]()
Ответ: ![]() ,
, ![]() ,
, ![]() .
.
3А. Теоремы сложения и умножения вероятностей.
Задача 3.1. Производится два броска по баскетбольному кольцу. Вероятности попадания при первом и втором бросках равны соответственно 0.3 и 0.8. Найти вероятность того, что в результате этих бросков в кольцо будет ровно одно попадание.
Решение
Введем события:
А - в результате этих бросков в кольцо будет ровно одно попадание.
А1 – первый раз мяч попал в кольцо,
А2 – второй раз мяч попал в кольцо,
И соответственно:
![]() – первый раз мяч не попал в кольцо
– первый раз мяч не попал в кольцо
![]() – второй раз мяч не попал в кольцо
– второй раз мяч не попал в кольцо
Тогда, событие А произойдет, если произойдут события А1 и ![]() или
или ![]() и
и ![]() .
.
Тогда по теоремам сложения и умножения вероятностей независимых событий, искомую вероятность можно найти по формуле
![]()
Таким образом,
![]()
Ответ: ![]()
5А. Закон распределения дискретной случайной величины и ее числовые характеристики.
Задача 5.1. По баскетбольному кольцу производится два независимых друг от друга броска. Вероятность попадания в кольцо при первом броске равна 0.6, втором – 0.7. Составить ряд распределения и найти математическое ожидание ![]() числа попаданий в кольцо при двух бросках.
числа попаданий в кольцо при двух бросках.
Решение
Случайная величина Х – число попаданий мячом в кольцо при двух бросках. Она может принимать значения 0, 1, 2. Найдём соответствующие вероятности:
При х=0 – два промаха. Вероятность промаха при первом броске 1-0,6=0,4, при втором броске 1-0,7=0,3. По теореме умножения вероятностей независимых событий: ![]()
При х=2 – оба попадания. Вероятность попадания в кольцо при первом броске равна 0.6, втором – 0.7. По теореме умножения вероятностей независимых событий: ![]()
При х=1 – одно попадание и один промах. Так как события один промах одно попадание, оба промаха и оба попадания образуют полную группу событий то искомую вероятность найдём по формуле:
![]()
Получили ряд распределения
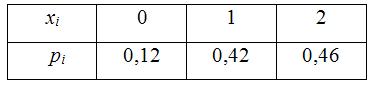
Найдём математическое ожидание числа попаданий в кольцо при двух бросках:
![]()
Ответ: ![]()
6А. Закон распределения непрерывной случайной величины и ее числовые характеристики.
Задача 6.1. Случайная величина ![]() имеет плотность распределения
имеет плотность распределения
 . Найти числовые характеристики случайной величины
. Найти числовые характеристики случайной величины ![]() .
.
Решение
Математическое ожидание находим по формуле
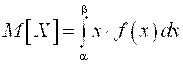 :
:
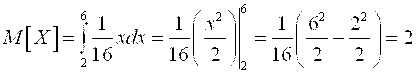
Дисперсию найдем по формуле ![]() :
:
 ,
,
Тогда 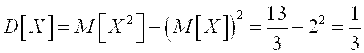 .
.
Среднее квадратическое отклонение: ![]()

Контрольные задания
ІІ. Математическая статистика
13А. Выборочный метод математической статистики
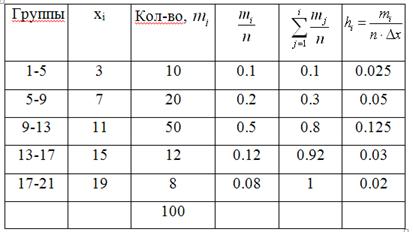
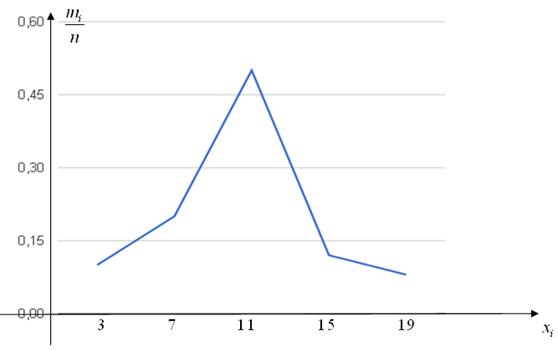
Пример 13.1. Построить полигон и гистограмму относительных частот по данному распределению

Решение
Объем выборки ![]() , длина интервала
, длина интервала ![]() . Для построения гистограммы относительных частот дополним заданную таблицу следующими строками: строкой, в которой расположим средние точки
. Для построения гистограммы относительных частот дополним заданную таблицу следующими строками: строкой, в которой расположим средние точки ![]() каждого интервала, строкой относительных частот
каждого интервала, строкой относительных частот ![]() , строкой накопленных относительных частот
, строкой накопленных относительных частот 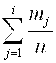 и строкой, в которой вычислим высоты столбиков гистограммы относительных частот
и строкой, в которой вычислим высоты столбиков гистограммы относительных частот 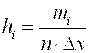 .
.
Построим гистограмму относительных частот, для этого на каждом интервале группированной выборки строим столбики, высоты которых вычислены в 6 столбце таблицы.
График гистограммы изображен на рис.
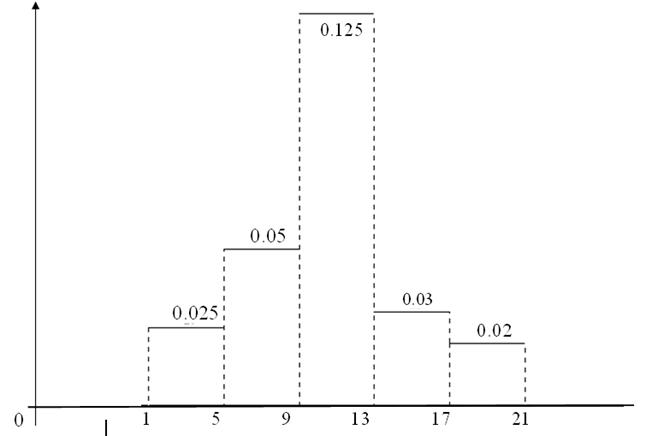
Строим полигон:
14А. Статистические оценки параметров распределения.
14.1.Точечные оценки параметров распределения
Примеры 1.– 10. Испытано 12 однотипных микросхем и с точностью до 1.0 часа зарегистрировано время безотказной работы каждой из них. Результаты испытаний сведены в таблицу:

Найти оценку математического ожидания ![]() и дисперсии
и дисперсии![]()
Решение
1.Для оценки математического ожидания ![]() используем формулу
используем формулу
![]()
В нашем случае ![]() 2. Оценку для дисперсии
2. Оценку для дисперсии ![]() проведём:
проведём:
А) когда известно математическое ожидание ![]() = 130 [час].
= 130 [час].
Используем формулу 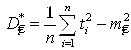
В нашем случае:  б) когда неизвестно математическое ожидание
б) когда неизвестно математическое ожидание ![]() .
.
В этом случае используем статистическое математическое ожидание![]() и формулу
и формулу 
В нашем случае:

14.2. Интервальная оценка параметров распределения
Определить доверительный интервал![]() .
.
Примеры 1.– 10. Построить 95-процентный (β=0.95) доверительный интервал ![]() для оценки неизвестного математического ожидания
для оценки неизвестного математического ожидания ![]() Случайной величины
Случайной величины ![]() , если по результатам N = 101 измерений получены оценки
, если по результатам N = 101 измерений получены оценки ![]()
![]()
Решение
Используем формулу для доверительного интервала
![]()
![]()
Значение табличной функции![]() положим
положим ![]()
В нашем случае ![]()
Тогда ![]()
Определить доверительный интервал![]() .
.
Примеры 1.– 10. Построить 96-процентный (β=0.95) доверительный интервал ![]() для оценки неизвестной дисперсии
для оценки неизвестной дисперсии ![]() случайной величины
случайной величины ![]() по результатам N = 101 измерений.
по результатам N = 101 измерений.
Решение
Оценку для дисперсии ![]() проведём:
проведём:
А) когда известно математическое ожидание ![]() и
и
![]()
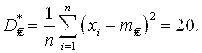
Используем формулу 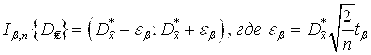 Значение табличной функции
Значение табличной функции ![]() положим
положим ![]()
В нашем случае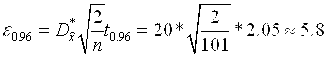
Тогда ![]()
Б) когда неизвестно математическое ожидание ![]() и
и

Используем формулу 
В нашем случае 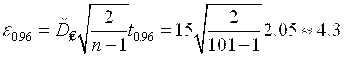
Тогда ![]()
16А. Определение характеристик случайных величин и построение линий регрессии по данным выборки
Примеры 1.10. Дана выборка объёма ![]() , заданная в таблицах №№1–10. Номер таблицы определяется последней цифрой зачётной книжки.
, заданная в таблицах №№1–10. Номер таблицы определяется последней цифрой зачётной книжки.
Требуется: вычислить выборочные средние, выборочные дисперсии, средние квадратические отклонения, корреляционный момент и коэффициент корреляции. Составить уравнение линии регрессии ![]() . Построить график линии регрессии относительно точек
. Построить график линии регрессии относительно точек ![]() таблицы. Найти остаточную дисперсию.
таблицы. Найти остаточную дисперсию.
таблица №1

Решение
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε - случайная ошибка (отклонение, возмущение).
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т. к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
Формально критерий МНК можно записать так:
S = ∑(yi - y*i)2 → min
Система нормальных уравнений.
A•n + b∑x = ∑y
A∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
5a + 10 b = 10.5
10 a + 30 b = 33
Из первого уравнения выражаем А и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 1.2, a = -0.3
Уравнение регрессии (эмпирическое уравнение регрессии):
Y = 1.2 x - 0.3
Эмпирические коэффициенты регрессии A и B являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу
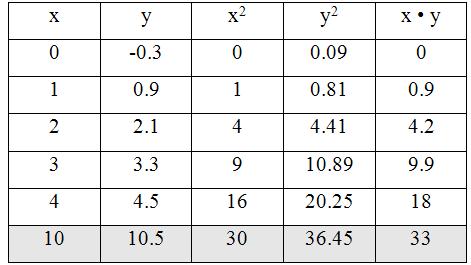
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
Ковариация. (корреляционный момент)
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X весьма высокая и прямая.
Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 1.2x - 0.3
Для оценки качества параметров регрессии построим расчетную таблицу:
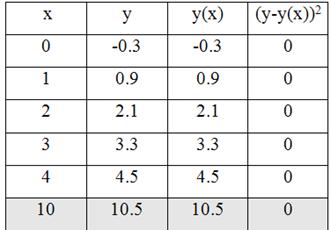
Остаточная дисперсия
![]()
В нашем случае 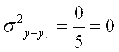
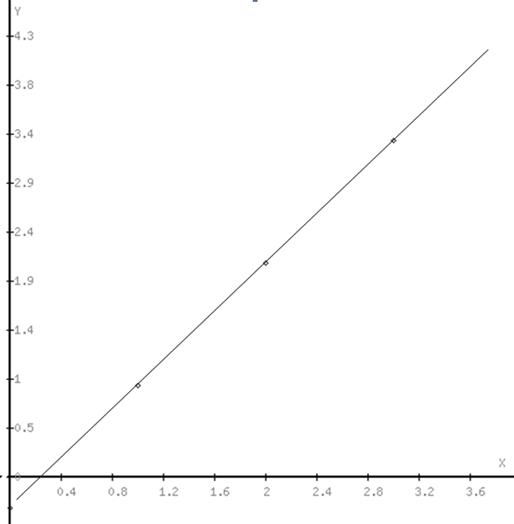
Построим график линии регрессии относительно точек ![]() таблицы.
таблицы.
| < Предыдущая | Следующая > |
|---|