Теория функции комплексного переменного 02
Задание 2.
Записать в алгебраической форме все элементы множества Е.
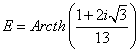 .
.
Множество 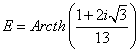 состоит из всех комплексных чисел z таких, что
состоит из всех комплексных чисел z таких, что ![]() .
.
Известно, что ![]() .
.
Обозначим ![]() . Получаем уравнение:
. Получаем уравнение:
![]() ,
,
![]() ,
,
![]()
![]()
Отсюда
![]()
Z=
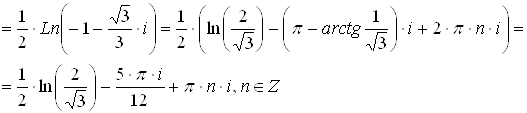
Ответ: 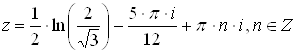
Задание 4.
Дана функция ![]() и множество
и множество ![]() .
.
1) Изобразить множество ![]() на комплексной плоскости.
на комплексной плоскости.
2) Найти образ ![]() множества
множества ![]() при отображении
при отображении ![]() (описать множество
(описать множество ![]() С помощью неравенств) и изобразить его на комплексной плоскости.
С помощью неравенств) и изобразить его на комплексной плоскости.
![]() ,
, 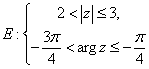
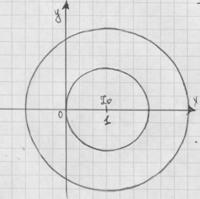
1) Изобразим множество
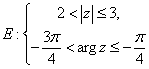
Первому неравенству соответствует кольцо с центром в точке ![]() и радиусами 2 и 3, причем окружность радиусом 2 не входит в область, а окружность радиусом 3 входит.
и радиусами 2 и 3, причем окружность радиусом 2 не входит в область, а окружность радиусом 3 входит.
Второму неравенству соответствует угол между лучами ![]() и
и ![]() .
.
Луч ![]() не входит в область,
не входит в область, ![]() входит.
входит.
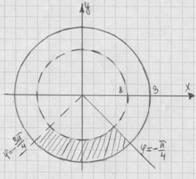
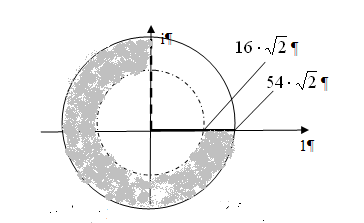
2) ![]()
А) ![]()
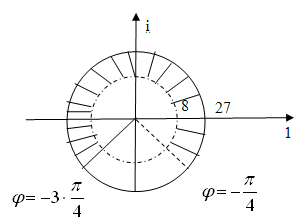
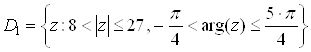
Б) ![]()
![]() - коэффициент растяжения функции.
- коэффициент растяжения функции.
![]() - угол поворота
- угол поворота
Тогда получим область
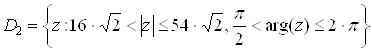
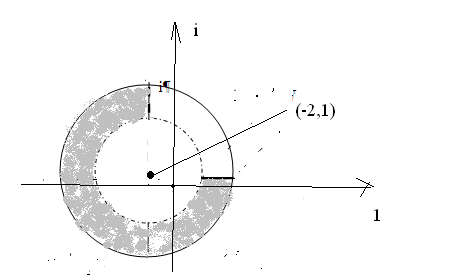
В)![]() . Это есть перенос на (-2+i).
. Это есть перенос на (-2+i).
Получим искомую область Е/:
Задание 5.
Дана функция ![]() И точка
И точка ![]() .
.
1) Найти все возможные разложения функции ![]() в ряд Лорана (ряд Тейлора) по степеням
в ряд Лорана (ряд Тейлора) по степеням ![]() . Указать области, в которых справедливы полученные разложения.
. Указать области, в которых справедливы полученные разложения.
2) Определить, является ли точка ![]() изолированной особой точкой функции
изолированной особой точкой функции ![]() . Если да, то, используя разложение функции
. Если да, то, используя разложение функции ![]() в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки ![]() , определить тип особой точки
, определить тип особой точки ![]() и найти вычет функции
и найти вычет функции ![]() в этой точке.
в этой точке.
3) Используя разложение функции ![]() в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки ![]() , определить тип особой точки
, определить тип особой точки ![]() и найти вычет функции
и найти вычет функции ![]() в этой точке.
в этой точке.
![]() ,
, ![]() .
.
Решение.
1) Представим дробь ![]() в виде суммы простых дробей, т. е.
в виде суммы простых дробей, т. е. ![]() .
.
Найдем коэффициенты A, B и С.
![]() ,
,
![]() ,
,
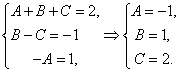
Получили ![]() .
.
У функции три особые точки ![]() ,
, ![]() И
И ![]() .
.
Получим три кольца с центром в точке ![]() (совпадает с особой точкой), в каждой из которой функция
(совпадает с особой точкой), в каждой из которой функция ![]() является аналитической:
является аналитической:
I)![]() ;
;
II)![]() ;
;
III)![]() .
.
А) Преобразуем дроби к нужному виду
![]() ,
,
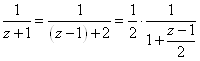 .
.
Используем разложение ![]() ,
, ![]() .
.
Значит при ![]() и при
и при ![]() , т. е. при
, т. е. при ![]() и
и ![]() При можно получить разложения полученных выражений в ряд:
При можно получить разложения полученных выражений в ряд:
![]()
![]()
=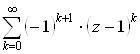 .
.
Аналогично,
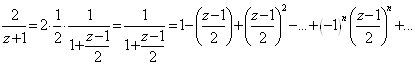 .=
.=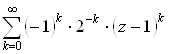
Значит, в кольце ![]() Получим первое разложение в ряд Лорана:
Получим первое разложение в ряд Лорана:
![]() .=
.=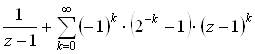
Б) При ![]() и при
и при ![]()
Используем представления:
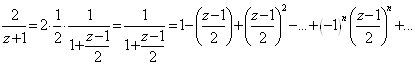 .=
.=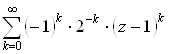
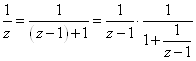 =
=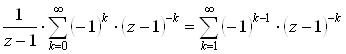
Поэтому в кольце ![]() имеем:
имеем:
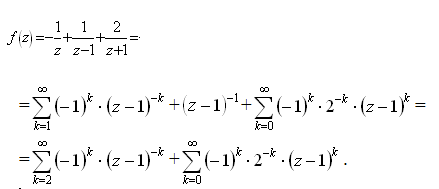
С) при ![]()
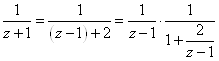 .=
.=
=[ Используем разложение ![]() ,
, ![]() .]=
.]=
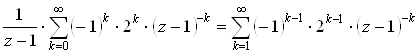
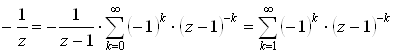
Поэтому
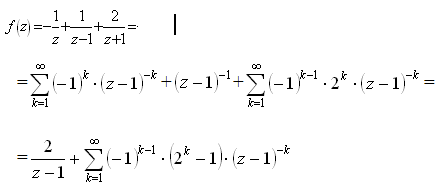
2) Точка ![]() является изолированной особой точкой функции
является изолированной особой точкой функции ![]() .
.
Используем разложение
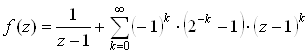
В точке ![]() функция имеет простой полюс и вычет равен коэффициенту при
функция имеет простой полюс и вычет равен коэффициенту при ![]() , т. е. вычет равен 1.
, т. е. вычет равен 1.
3) Точка ![]() является устранимой особой точкой.
является устранимой особой точкой.
Для нахождения вычета в данной точке получим разложение функции в ряд Лорана в окрестности этой точки. Имеем:
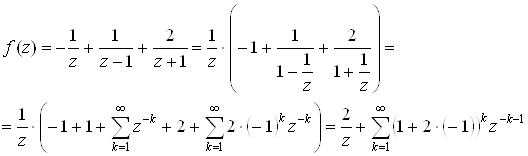
Поэтому ![]() .
.
Задание 6.
Дана функция ![]() и дано число
и дано число ![]() .
.
1) Разложить функцию ![]() в ряд Лорана по степеням
в ряд Лорана по степеням ![]() .
.
2) Используя разложение функции ![]() в ряд Лорана, определить тип особой точки
в ряд Лорана, определить тип особой точки ![]() и найти вычет функции
и найти вычет функции ![]() в этой точке.
в этой точке.
3) Используя разложение функции ![]() в ряд Лорана, определить тип особой точки
в ряд Лорана, определить тип особой точки ![]() и найти вычет функции
и найти вычет функции ![]() в этой точке.
в этой точке.
![]() ,
, ![]() .
.
Решение.
1) Функция аналитическая при всех ![]() .
.
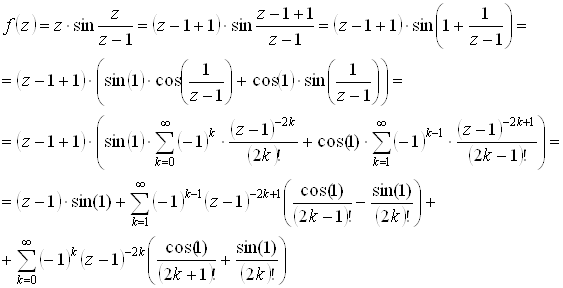
Точка ![]() - существенно особая, так как главная часть ряда Лорана бесконечна.
- существенно особая, так как главная часть ряда Лорана бесконечна.
Имеем ![]() - величина вычета в точке z=1/
- величина вычета в точке z=1/
Получим теперь ряд Лорана в точке ![]() . Имеем:
. Имеем:
Рассмотрим ![]()
Имеем

Получаем ряд Тейлора в точке ![]()
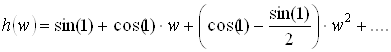
Тогда 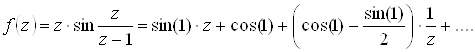
- ряд Лорана в точке ![]() . Получаем
. Получаем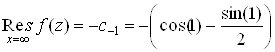
Задание 7.
Найти интеграл ![]() с помощью вычетов. Кривая Г ориентирована против часовой стрелки.
с помощью вычетов. Кривая Г ориентирована против часовой стрелки.
 ,
, ![]() .
.
Решение.
Функция ![]() имеет особые точки
имеет особые точки ![]() .
. ![]()
Проверяем, какие из них принадлежат исходной области:
![]()
![]()
![]()
Получается, что в круге ![]() лежат все особые точки
лежат все особые точки ![]() .
. ![]()
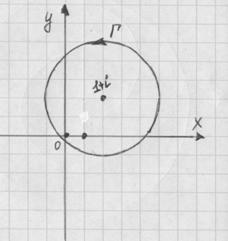
Так как ![]() -устранимая особая точка, то вычет в ней равен 0
-устранимая особая точка, то вычет в ней равен 0
Так как ![]() - полюс второго порядка, то по формуле нахождения вычетов будем иметь:
- полюс второго порядка, то по формуле нахождения вычетов будем иметь:

Так как ![]() - полюс первого порядка, то по формуле нахождения вычетов будем иметь:
- полюс первого порядка, то по формуле нахождения вычетов будем иметь:

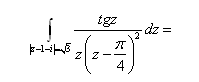
= 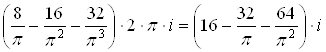
Ответ: 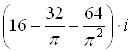
Проверка(маткад)
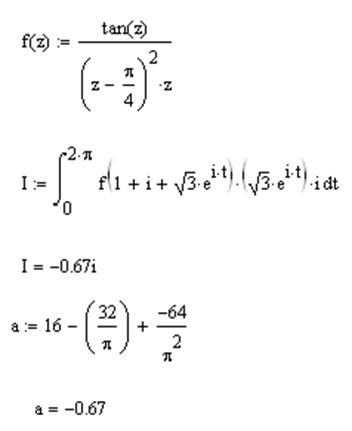
Задание 8.
Найти несобственный интеграл ![]() с помощью вычетов.
с помощью вычетов.
![]() ,
, ![]() .
.
Решение.
Рассмотрим уравнение ![]()
Или ![]()
Имеем 4 корня;
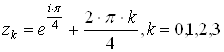
В верхней полуплоскости имеем 2 корня

Это простые полюсы подинтегральной функции.
Найдем вычеты в этих особых точках:


По теореме о вычетах с учетом леммы Жордана получим:
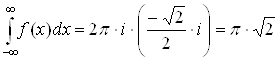
Поэтому
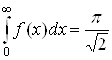
Ответ: ![]()
Проверка:
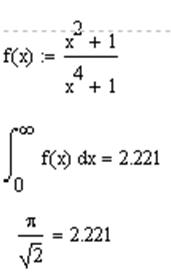
Задание 9.
Используя теорему Руше, найти число нулей функции ![]() в области
в области ![]() (каждый нуль считается столько раз, какова его кратность).
(каждый нуль считается столько раз, какова его кратность).
![]() ,
, ![]() .
.
Решение.
Пусть ![]() , где
, где ![]() и
и ![]() .
.
При ![]() , имеем
, имеем ![]() , ,
, , ![]() Т. е.
Т. е. ![]() .
.
По теореме Руше все шесть нулей функции ![]() лежат в круге
лежат в круге ![]() .
.
Определим, сколько из них имеют модуль меньше 1.
Пусть ![]() . При
. При ![]() имеем
имеем ![]() . Поэтому в круге
. Поэтому в круге ![]() функция
функция ![]() имеет столько же нулей сколько и функция
имеет столько же нулей сколько и функция ![]() , т. е. 1 нуль. Поэтому в кольце
, т. е. 1 нуль. Поэтому в кольце ![]() функция
функция ![]() имеет 6-1=5 нулей.
имеет 6-1=5 нулей.
Ответ: 5 нулей.
Проверка:

Задание 10.
С помощью вычетов найти оригинал ![]() изображения
изображения ![]() . Сделать проверку (найти изображение функции
. Сделать проверку (найти изображение функции ![]() , используя таблицу стандартных изображений и свойства преобразования Лапласа и убедиться, что оно равно
, используя таблицу стандартных изображений и свойства преобразования Лапласа и убедиться, что оно равно ![]() )
)
 .
.
Решение.
![]() .
.
Рассмотрим функцию 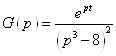 .
.
Найдем корни уравнения ![]() ,
,
![]() ,
, ![]() ,
, ![]() - это особые точки второго порядка для данной функции.
- это особые точки второго порядка для данной функции.
Найдем вычеты в особых точках

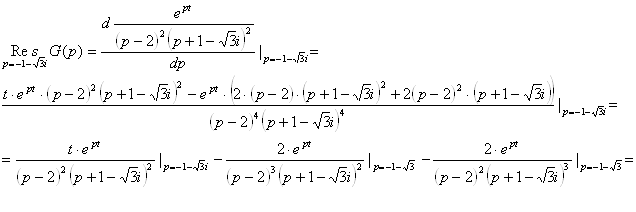 Данные вычисления очень громоздки и при ручном вычислении в них легко допустить ошибку.
Данные вычисления очень громоздки и при ручном вычислении в них легко допустить ошибку.
Воспользуемся Мапл:
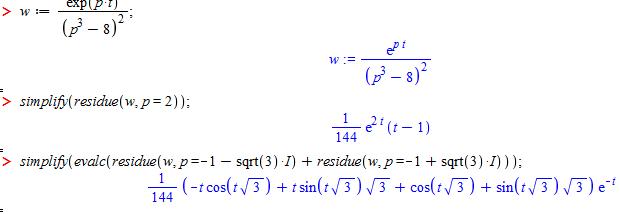
Итак, оригинал имеет вид:
![]()
Этот же результат легко получить независимо в маткаде:
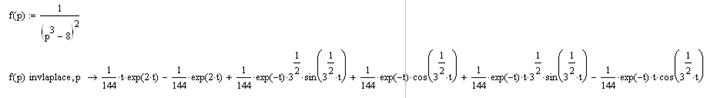
Так как независимые пакеты дали одинаковый результат корректность ответа установлена.
| < Предыдущая | Следующая > |
|---|