Циркуляция и поток векторного поля

Задача 1. Найдите циркуляцию векторного поля вдоль контура Г: , , лежащего в плоскости , в положительном направлении относительно орта K.

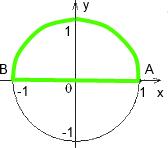
Решение. Способ 1. Контуром интегрирования Г является АВА: половина окружности радиуса 1 с центром в начале координат и отрезок прямой .

По формуле Стокса имеем

За поверхность S, ограниченную контуром Г, примем полукруг образованный сечением кругового цилиндра плоскостью .

Следовательно,

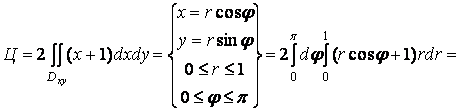
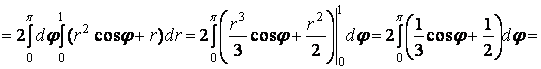
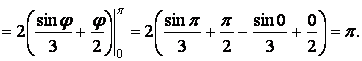
Ответ: .

Способ 2. Можно было решать по определению.

Циркуляция векторного поля вдоль контура Г определяется формулой линейного интеграла вдоль замкнутой линии Г:

Дуга АВ является частью окружности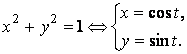

Вычисляем

Получаем:

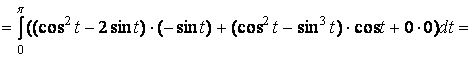
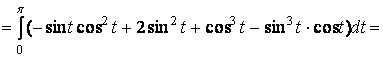
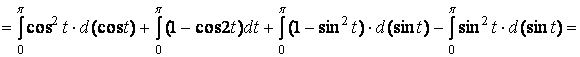
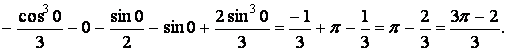
Окончательно,

Ответ: .

Задача 2. Найдите поток векторного поля через замкнутую поверхность , , в направлении внешней нормали.

Решение. Поверхностью является пирамида V, образованная плоскостью и координатными плоскостями.

Проекция поверхности на плоскость XOY есть треугольник D, ограниченный прямыми , ,

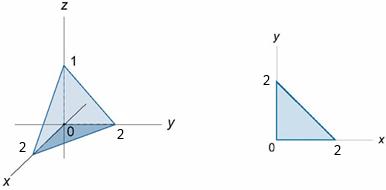
Так как поверхность замкнутая, то можем воспользоваться формулой Остроградского-Гаусса:

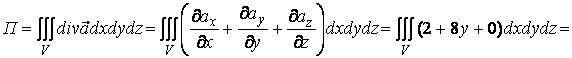
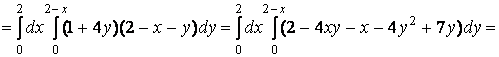
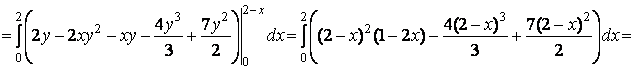
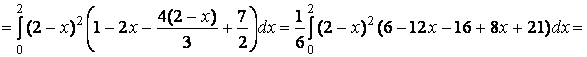
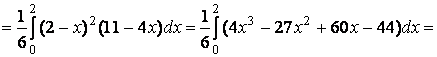
Ответ: .

< Предыдущая		Следующая >