Решение игры симплекс-методом
Пример. Найти решение матричной игры с платежной матрицей:

Решение. Матричной игре с данной платежной матрицей будет соответствовать пара двойственных задач линейного программирования:
Найти минимум функции F(Х) = x1 + x2 + x3 при ограничениях:
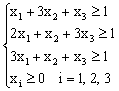
Найти максимум функции T(Y) = y1 + y2 + y3 при ограничениях:
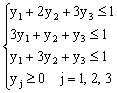
Здесь
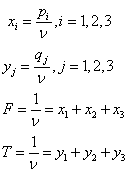
Решаем последнюю задачу симплексным методом.
|
Базисные перемен- Ные |
|
|
|
|
|
|
ДО | |
|
|
1 |
1 |
2 |
3 |
1 |
0 |
0 |
1 |
|
|
1 |
3 |
1 |
1 |
0 |
1 |
0 |
|
|
|
1 |
1 |
3 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 | |
|
|
|
0 |
5/3 |
|
1 |
|
0 |
|
|
|
|
1 |
1/3 |
|
0 |
|
0 |
1 |
|
|
2/3 |
0 |
8/3 |
2/3 |
0 |
-1/3 |
1 |
|
|
|
|
0 |
-2/3 |
|
0 |
|
0 | |
|
|
1/4 |
0 |
0 |
9/4 |
1 |
-1/8 |
-5/8 |
|
|
|
|
1 |
0 |
1/4 |
0 |
|
|
1 |
|
|
|
0 |
1 |
1/4 |
0 |
|
|
1 |
|
|
|
0 |
0 |
-1/2 |
0 |
|
| |
|
|
|
0 |
0 |
1 |
|
|
| |
|
|
|
1 |
0 |
0 |
|
|
| |
|
|
|
0 |
1 |
0 |
|
|
| |
|
|
|
0 |
0 |
0 |
|
|
| |
|
|
|
|
|
|
|
Решение этой задачи
![]() .
.
Тогда цена игры ![]() а вероятности применения стратегий игрока II будут:
а вероятности применения стратегий игрока II будут:
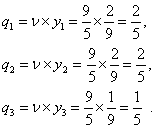
Из симплекс-таблицы находим решение двойственной задачи:
![]()
Следовательно, вероятности применения стратегий игрока I:
![]() ,
,
Таким образом, оптимальные смешанные стратегии игроков:
![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|