Контрольная работа по мат. анализу 23
Вариант 2
Задания для контрольной работы №1
1. Введение в анализ. Дифференциальное исчисление
1-10. Найти пределы функций.
2. 1)![]() при A)
при A) ![]() , B)
, B) ![]() , C)
, C) ![]() ;
;
2) ![]() 3)
3) ![]() ; 4)
; 4) ![]()
1)![]()
![]()

2) 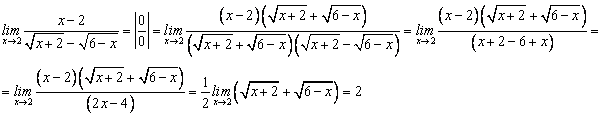 3)
3) ![]() ;
;
Использовали ![]() при
при ![]()
4) 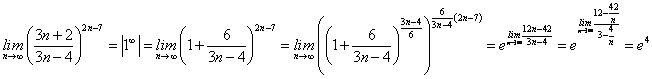
11-20. Найти производные заданных функций.
12. А) ![]() ; Б)
; Б) ![]()
В) ![]() Г)
Г) ![]() .
.
А) 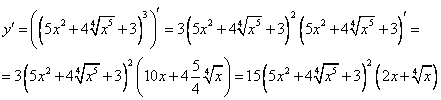
Б) 
В) 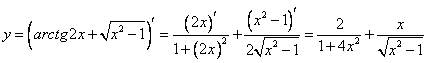
Г)  .
.
21-30. Вычислить приближенное значение ![]() , заменив в точке
, заменив в точке ![]() приращение функции
приращение функции ![]() дифференциалом.
дифференциалом.
22. ![]()
![]()
![]()
Решение
Имеем ![]() , то есть
, то есть ![]()
В нашем случае ![]() ,
, ![]()
![]()
Отсюда: ![]()
![]()
Поэтому ![]() ,
, ![]()
31-40. Исследовать функцию ![]() и построить ее график.
и построить ее график.
32. ![]()
Решение
Исследуем функцию, заданную формулой: ![]()
Область определения:
Найдём первую производную:
 =
=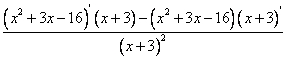 =
=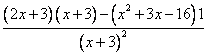 ==
== =
=
Первая производная: 
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение.
 ,
, ![]() ,
, ![]()
Дискриминант отрицателен, значит уравнение не имеет корней.
Критические точки: нет
Найдём вторую производную:
Вторая производная это производная от первой производной.
 =
= =
=
= =
=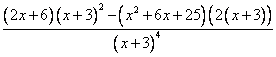 =
=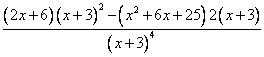 =
=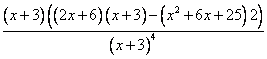 =
=
=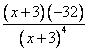 =
=![]()
Вторая производная: ![]()
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
- нет решений.
Возможные точки перегиба: нет
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
![]() ,
, ![]() ,
, ![]()
![]() ;
;![]()
Точки пересечения с осью : ![]()
Пусть, ![]() . Точки пересечения с осью :
. Точки пересечения с осью :
Определим значения аргумента, при которых знаменатель функции обращается в ноль
, . Вертикальные асимптоты:
Горизонтальные асимптоты: нет.
Для нахождения наклонных асимптот преобразуем исходное выражение. ![]() =
=![]() =
=![]()
Наклонные асимптоты: .
Предел разности исходной функции и функции на бесконечности равен нулю.
Точки разрыва:
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)=f(x).
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
Тестовые интервалы:

Результаты исследования функции занесем в таблицу.
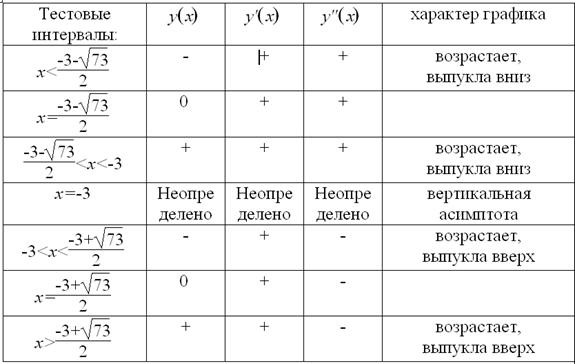
Относительные экстремумы: нет
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
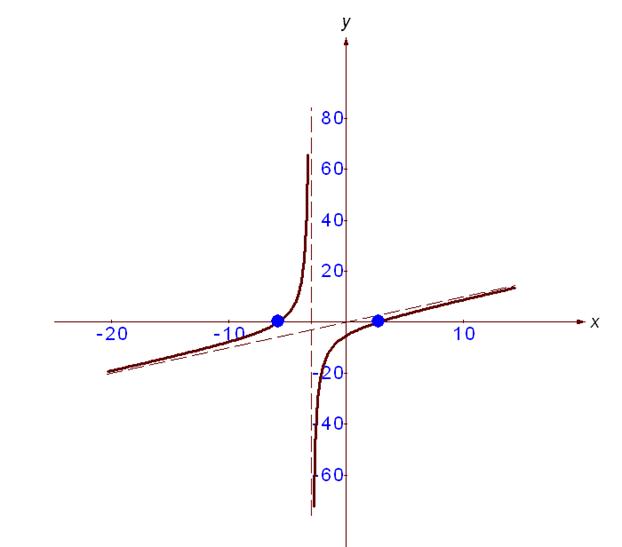
41-50. Найти неопределенные интегралы. Результаты проверить дифференцированием.
42. а) ![]() ; Б)
; Б) ![]() ;
;
Решение
А)  ;
;
Проверка: 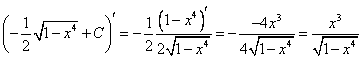 верно
верно
Б) 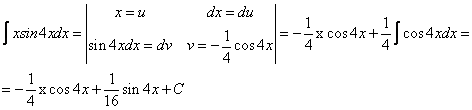 ;
;
Проверка: 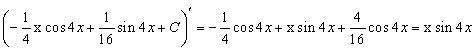 верно
верно
51-60. Вычислить по формуле Ньютона-Лейбница определенный интеграл 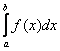 .
.
52. 
Решение
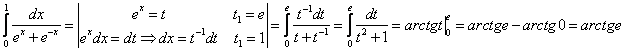
61-70. Вычислить площадь фигуры, ограниченной параболой ![]() и прямой
и прямой ![]() . Сделать чертеж.
. Сделать чертеж.
62. ![]()
![]()
Решение
Изобразим фигуру, площадь которой нужно найти:

Найдём абсциссы точек пересечения данных линий, для этого решим систему уравнений:
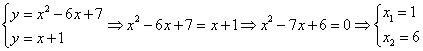 ,
,
По формуле ![]() . В нашем случае
. В нашем случае ![]() ,
,![]() ,
, ![]() ,
, ![]() . Получим:
. Получим:
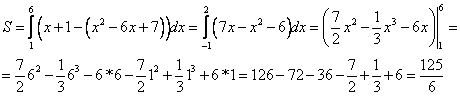
Ответ: ![]() (кв. ед)
(кв. ед)
Задания для контрольной работы № 2
1. Аналитическая геометрия
1-10. Даны вершины ![]()
![]()
![]() треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
2. А(1;1), В (7;4), С (4;5)
Решение
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: , где a1a2 = X1X2 + Y1Y2
Найдем угол между векторами AB(6;3) и AC(3;4)
, γ = arccos(0.89) = 26.570
Уравнение медианы треугольника
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
, , M(4;5/2)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(4;5) и М(4;5/2), поэтому:
Каноническое уравнение прямой:
или или x - 4 = 0 или x = 4
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
, , y = -2x + 13 или y +2x -13 = 0
Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Принимая A за первую вершину, находим:
По формуле получаем:
11-20. Решить систему линейных уравнений матричным способом
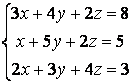
Решение
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов: , Вектор B: BT=(8,5,3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=3•(5•4-3•2)-1•(4•4-3•2)+2•(4•2-5•2)=28
Итак, определитель 28 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
Тогда:
Где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) N-1 порядка, полученный вычеркиванием I-й строки и J-го столбца в определителе матрицы А.
Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения.
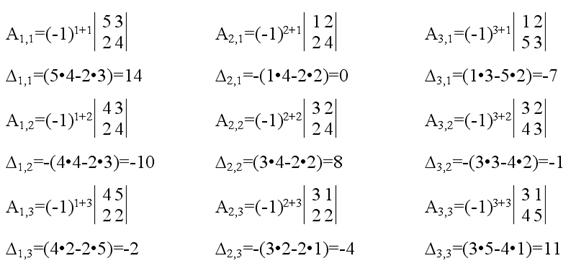
Из полученных алгебраических дополнений составим присоединенную матрицу:
Вычислим обратную матрицу:
Вектор результатов X X=A-1 • B,
, ,
XT=(2,1,-1)
X=56 / 28=2
У=28 / 28=1
Z=-28 / 28=-1
Ответ: x=2, у=1 , z=-1
Вариант 7
Задания для контрольной работы №1
1. Введение в анализ. Дифференциальное исчисление
1-10. Найти пределы функций.
7. 1) ![]() при A)
при A) ![]() , B)
, B) ![]() , C)
, C) ![]() ;
;
2) ![]() 3)
3) ![]() ; 4)
; 4) ![]()
Решение
1) ![]()
![]()
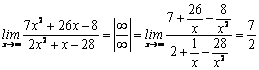
2) 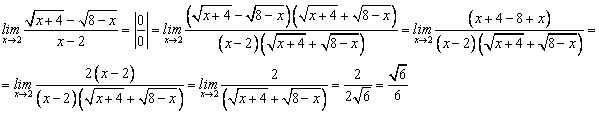 3)
3) ![]() ;
;
Использовали ![]() при
при ![]()
4) 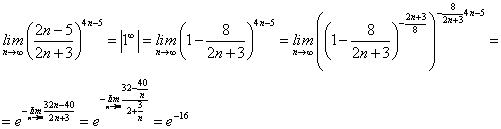
11-20. Найти производные заданных функций.
17. А)  ; Б)
; Б) 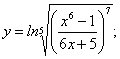
В) ![]() Г)
Г) ![]() .
.
Решение
А) 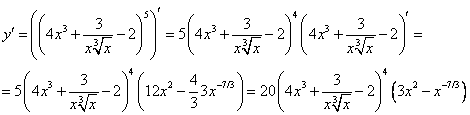 ;
;
Б)  В)
В) 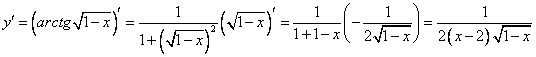
Г) 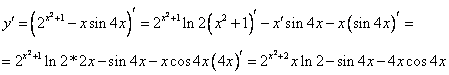 .
.
21-30. Вычислить приближенное значение ![]() , заменив в точке
, заменив в точке ![]() приращение функции
приращение функции ![]() дифференциалом.
дифференциалом.
27. ![]()
![]()
![]()
Решение
Имеем ![]() , то есть
, то есть ![]()
В нашем случае ![]() ,
, ![]()
![]()
Отсюда: ![]()
![]()
Поэтому ![]() ,
, ![]()
31-40. Исследовать функцию ![]() и построить ее график.
и построить ее график.
37. ![]()
Решение
Исследуем функцию, заданную формулой: ![]()
Область определения:
Найдём первую производную:
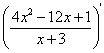 =
=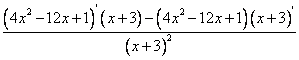 =
=
=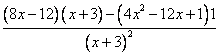 =
=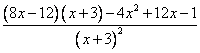 =
=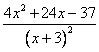
Первая производная: 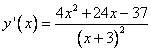
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение.
 ,
, ![]() ,
, ![]()
![]() ;
;![]()
Критические точки: ![]()
Найдём вторую производную:
Вторая производная это производная от первой производной.
 =
=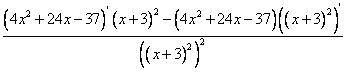 =
=
=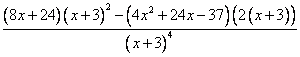 =
=
=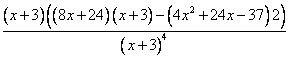 =
= =
=![]()
Вторая производная: ![]()
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. - нет решений.
Возможные точки перегиба: нет
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
![]() ,
, ![]() ,
, ![]()
![]() ;
;![]()
Точки пересечения с осью : ![]()
Точки пересечения с осью :
Пусть, ![]()
Определим значения аргумента, при которых знаменатель функции обращается в ноль
, Вертикальные асимптоты:
Горизонтальные асимптоты: нет.
Для нахождения наклонных асимптот преобразуем исходное выражение.
![]() =
=![]() =
=![]()
Наклонные асимптоты: .
Предел разности исходной функции и функции на бесконечности равен нулю.
Точки разрыва:
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)=f(x).
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
Тестовые интервалы:

Результаты исследования функции занесем в таблицу.
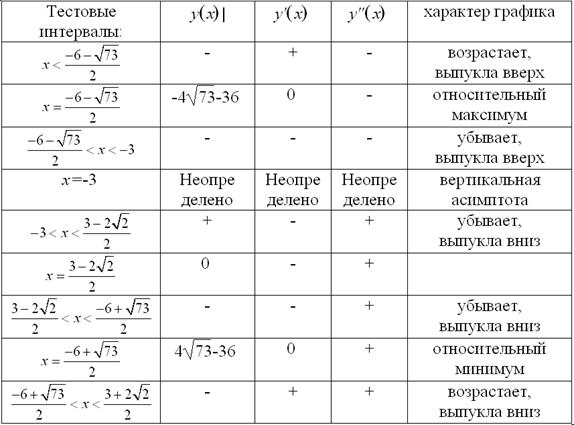
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум 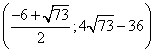 .
.
Проходя через точку максимума. производная функции меняет знак с (+) на (-). Относительный максимум  .
.
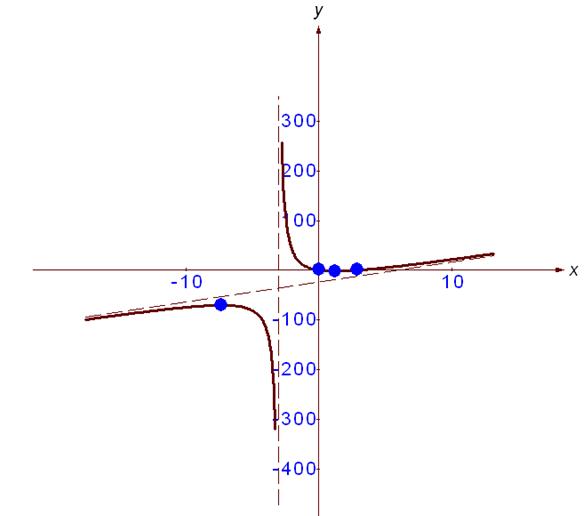
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
41-50. Найти неопределенные интегралы. Результаты проверить дифференцированием.
47. А) ![]() ; Б)
; Б) ![]() ;
;
Решение
А) 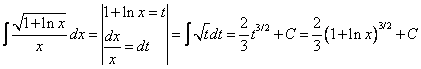 ;
;
Проверка: 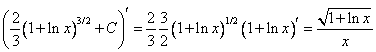 - верно
- верно
Б)  Проверка:
Проверка:  -верно
-верно
51-60. Вычислить по формуле Ньютона-Лейбница определенный интеграл 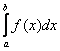 .
.
57. ![]()
Решение

61-70. Вычислить площадь фигуры, ограниченной параболой ![]() и прямой
и прямой ![]() . Сделать чертеж.
. Сделать чертеж.
67. ![]()
![]()
Решение
Изобразим фигуру, площадь которой нужно найти:
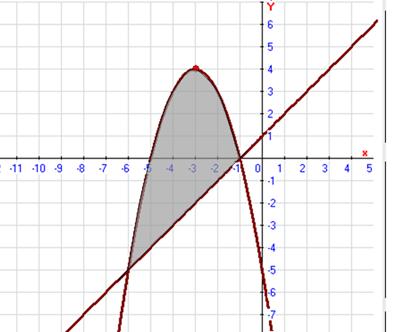
Найдём абсциссы точек пересечения данных линий, для этого решим систему уравнений:
 ,
,
По формуле ![]() . В нашем случае
. В нашем случае ![]() ,
,![]() ,
, ![]() ,
, ![]() . Получим:
. Получим:
 Ответ:
Ответ: ![]() (кв. ед)
(кв. ед)
Задания для контрольной работы № 2
1. Аналитическая геометрия
1-10. Даны вершины ![]()
![]()
![]() треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
7. А (1;6), В (7;4), С (4;5)
Решение
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: , где a1a2 = X1X2 + Y1Y2
Найдем угол между векторами AB(6;-2) и AC(3;-1)
, γ = arccos(1) = 00
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
, , M(4;5)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(4;5) и М(4;5), поэтому:
Каноническое уравнение прямой:
или или x - 4 = 0 или x = 4
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
, , y = 3x -7 или y -3x +7 = 0
Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Принимая A за первую вершину, находим:
По формуле получаем:
11-20. Решить систему линейных уравнений матричным способом

Решение
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов: , Вектор B: BT=(6,9,10)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=1•(1•2-5•4)-4•(2•2-5•3)+3•(2•4-1•3)=41
Итак, определитель 41 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
Тогда:
Где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) N-1 порядка, полученный вычеркиванием I-й строки и J-го столбца в определителе матрицы А.
Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения.
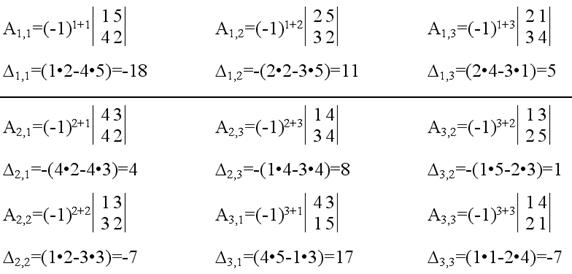
Из полученных алгебраических дополнений составим присоединенную матрицу:
Вычислим обратную матрицу:
Вектор результатов X X=A-1 • B
, ,
XT=(1,1,1)
X=41 / 41=1
Y=41 / 41=1
Z=41 / 41=1
Ответ: x=1, y=1, z=1
| < Предыдущая | Следующая > |
|---|