Контрольная работа по мат. анализу 16

Задания для контрольной работы №1

1–10. Решить уравнения и сделать проверку найденных корней уравнения

А)

Приведём к общему знаменателю

Сделаем проверку. Подставим найденные корни в исходное уравнение

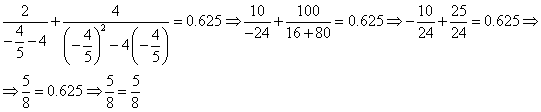
- верно

Б)

Возведём в квадрат обе части уравнения

Ещё раз возведём в квадрат обе части уравнения

Сделаем проверку. Подставим найденные корни в исходное уравнение

- не верно, - не корень

- верно

11–20. Выполнить действия с заданными матрицами

21–30. Найти решение системы линейных уравнений методом Крамера

Запишем систему в виде:, BT = (7,-5,8)

Главный определитель:

∆ = 1 • (3 • 3-2 • (-1))-0 • (1 • 3-2 • 2)+1 • (1 • (-1)-3 • 2) = 4 = 4

Заменим 1-ый столбец матрицы А на вектор результата В.

7	1	2
-5	3	-1
8	2	3

Найдем определитель полученной матрицы.

∆1 = 7 • (3 • 3-2 • (-1))-(-5 • (1 • 3-2 • 2))+8 • (1 • (-1)-3 • 2) = 16

Заменим 2-ый столбец матрицы А на вектор результата В.

1	7	2
0	-5	-1
1	8	3

Найдем определитель полученной матрицы.

∆2 = 1 • (-5 • 3-8 • (-1))-0 • (7 • 3-8 • 2)+1 • (7 • (-1)-(-5 • 2)) = -4

Заменим 3-ый столбец матрицы А на вектор результата В.

1	1	7
0	3	-5
1	2	8

Найдем определитель полученной матрицы.

∆3 = 1 • (3 • 8-2 • (-5))-0 • (1 • 8-2 • 7)+1 • (1 • (-5)-3 • 7) = 8

Выпишем отдельно найденные переменные Х: , ,

31–40. С помощью преобразования графиков основных элементарных функций построить графики функций.

А)

Строим

Строим - переносим график на еденицу влево

Строим - переносим график на 4 вниз.

Б)

Строим

Строим - переносим график на вправо

Строим - переносим график на 1 вверх.

40–50. Найти области определения для функций

А)

Область определения данной функции можно записать в виде системы неравенств

Решая неравенство методом интервалов получим

Следовательно, искомая область определения

Б)

Область определения данной функции можно записать в виде системы неравенств

Следовательно, искомая область определения

51–60. Решить графически уравнение

Чтобы решить графически уравнение с одним неизвестным, необходимо перенести все его члены в одну часть, т. e. привести к виду: f(x)=0 и построить график функции y=f(x). Абсциссы точек пересечения графика с осью Х будут корнями этого уравнения.

По графику видно что уравнение имеет два корня

Задания для контрольной работы №2

61–70. Найти предел функции.

А)

Б)

71–75. Количество электричества, протекающее через проводник, начиная с момента времени t=0 , определено зависимостью (Кл). Найти силу тока в конце T секунды. ,

Решение

Сила тока есть производная количества электричества по времени: следовательно, нужно найти производную функции

И вычислить ее значение при t=7c. Имеем , откуда при получим (A).

Ответ: 62(А)

81–90. Найти производные функций.

А)

б)

В)

91–100. Записать уравнение касательной к графику функции в точке графика с абсциссой . Сделать чертёж.

Решение

Уравнение касательной к графику функции в точке имеет вид . Тогда, в нашем случае:

Тогда окончательно .

Сделаем чертёж

111–120. Найти неопределённые интегралы.

А)

Б)

В)

121–125. Интеграл вычислить точно по формуле Ньютона-Лейбница и приближённо по формуле прямоугольников. Указать абсолютную и относительную погрешности приближённого значения.

Примечание. 1. Отрезок Разбить на 10 частей. Привести таблицу значений функции В точках разбиения.

2. Промежуточные вычисления вести с четырьмя знаками после запятой. Приближённое значение интеграла дать с округлением до третьего десятичного знака.

3. При решении этой задачи рекомендуется пользоваться вычислительными средствами.

Решение

Найдем точное значение интеграла:

Пусть , тогда разобъём отрезок интегрирования на 10 частей с шагом И составим таблицу, в которой найдены середины отрезков

И значение функции в этих точках

Теперь по формуле средних прямоугольников

Получим:

Абсолютная погрешность равна

Относительная погрешность равна

131–140. Найти площадь фигуры, ограниченной заданными линиями. Сделать чертёж. ,

Решение

Изобразим фигуру, площадь которой нужно найти:

Найдём абсциссы точек пересечения данных линий, для этого решим систему уравнений:

Тогда, по формуле , получим

Ответ: кв. ед.

< Предыдущая		Следующая >