Исключение доминируемых стратегий в теории игр
Рассмотрим игру m ´ n, заданную платежной матрицей:
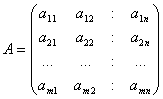 .
.
При постановке задач, необходимо иметь в виду некоторые преобразования, которые помогают упростить сложную задачу путем изменения – уменьшения размерности платежной матрицы посредством выделения и исключения доминируемых и дублирующих стратегий. Стратегия игрока Аi доминирует над стратегией Ак, если при любом поведении противника даст не меньший выигрыш, а если такой же, то дублирует Ак. В таком случае все элементы i строки больше (доминируют) или равны (дублируют) всех элементов строки k.
Пример. С учетом вариантов конъюнктуры В1, В2, В3, В4, В5 сложившейся на рынке и поведения покупателей в микрорайоне города коммерческое предприятие разработало шесть технологий продажи товаров А1, А2, А3, А4, А5, А6. Найти оптимальное решение. Возможные варианты среднедневного товарооборота в млн. руб. приведены в таблице:
|
В1 |
В2 |
В3 |
В4 |
В5 | |
|
А1 |
0,4 |
0,9 |
0,5 |
0,5 |
0,6 |
|
А2 |
0,6 |
0,5 |
0,7 |
0,8 |
0,9 |
|
А3 |
0,6 |
0,3 |
0,8 |
0,6 |
0,7 |
|
А4 |
0,3 |
0,8 |
0,5 |
0,4 |
0,3 |
|
А5 |
0,1 |
0,3 |
0,5 |
0,4 |
0,3 |
|
А6 |
0,4 |
0,8 |
0,5 |
0,4 |
0,5 |
Стратегия А1 доминирует над стратегией А6, а стратегия А4 доминирует над стратегией А5, следовательно исключаем 5 и 6 строки матрицы
|
В1 |
В2 |
В3 |
В4 |
В5 | |
|
А1 |
0,4 |
0,9 |
0,5 |
0,5 |
0,6 |
|
А2 |
0,6 |
0,5 |
0,7 |
0,8 |
0,9 |
|
А3 |
0,6 |
0,3 |
0,8 |
0,6 |
0,7 |
|
А4 |
0,3 |
0,8 |
0,5 |
0,4 |
0,3 |
С позиций проигрышей строки В стратегии В3, В4 и В5 доминируют над стратегией В1, поэтому эти столбцы исключаем из таблицы:
|
В1 |
В2 | |
|
А1 |
0,4 |
0,9 |
|
А2 |
0,6 |
0,5 |
|
А3 |
0,6 |
0,3 |
|
А4 |
0,3 |
0,8 |
С позиций игрока А стратегия А1 доминирует над стратегией А4, а стратегия А2 доминирует над стратегией А3, следовательно исключаем 3 и 4 строки матрицы:
|
В1 |
В2 | |
|
А1 |
0,4 |
0,9 |
|
А2 |
0,6 |
0,5 |
| < Предыдущая | Следующая > |
|---|