Экстремумы, предел, дифференциальное уравнение

1 задача: найти промежутки монотонности и точки экстремума функции

Решение:

Находим производную функции:

Находи точки, в которых производная равна 0:

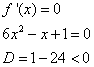
Т. к. дискриминант квадратного уравнения отрицателен, то данное уравнение корней не имеет. Т. к. коэффициент при больше 0, то выражение , т. е. положительно при всех значениях х. Следовательно, функция монотонно возрастает на всей числовой оси. Точек экстремума функция не имеет.

2 задача: вычислить предел при х стремится к х от функции

Решение:

Имеет место неопределенность вида . Вынесем в числителе и знаменателе за скобки ч в наибольшей степени:

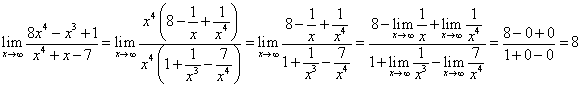
3 задача: решить дифференциальное уравнение

Решение:

Данное уравнение является однородным уравнением, т. к.

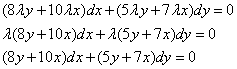
Для решения однородного уравнения воспользуемся заменой: . Откуда получаем уравнение:

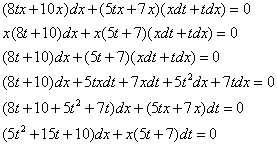
Получили уравнение с разделяющимися переменными.

Выполним разделение переменных:

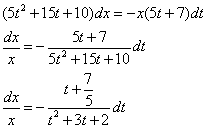
Интегрируем обе части:

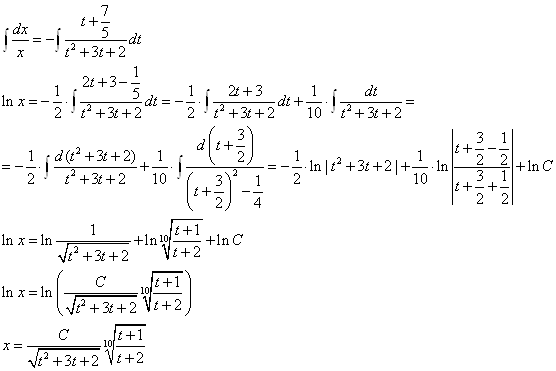
Вернемся к замене:

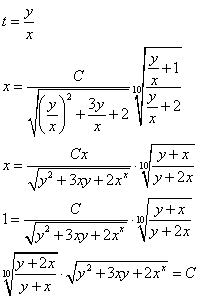
< Предыдущая		Следующая >