Дифференциальное и интегральное исчисление 02
Вариант 10
Задача 1
С помощью определения предела последовательности показать, что данная последовательность ![]() при
при ![]() имеет своим пределом число А. Найти целое значение N, Начиная с которого
имеет своим пределом число А. Найти целое значение N, Начиная с которого ![]() .
.
![]()
![]()
![]()
Рассмотрим неравенство
![]()
![]() - натуральное
- натуральное
Откуда ![]() ,
, ![]() .
.
Следовательно, ![]()
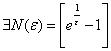
![]()
![]() , где квадратные скобки обозначают целую часть числа. То есть, число 0 является пределом последовательности. Пусть теперь
, где квадратные скобки обозначают целую часть числа. То есть, число 0 является пределом последовательности. Пусть теперь ![]() . Тогда
. Тогда ![]()
Задача 2
Вычислить предел ![]()

Задача 3
Вычислить производную ![]()
![]()
Решение

Задача 4
Вычислить производную ![]()
![]()
Решение

Задача 5
Вычислить логарифмическую производную ![]()
![]()
Решение
Имеем ![]()
![]()

Задача 6
Вычислить производную ![]() функции, заданной параметрически.
функции, заданной параметрически.
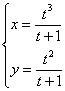
Решение
По формуле ![]() имеем
имеем



Задача 7
Вычислить производную ![]() функции, заданной неявно уравнением
функции, заданной неявно уравнением ![]()
![]()
Решение
По формуле ![]() .
.
Имеем ![]() ,
,
![]()
Отсюда легко находим ![]() :
:
![]()
Задача 8
Найти предел, используя правило Лопиталя.
![]()
Решение
Неопределённость типа ![]() . Используем правило Лопиталя
. Используем правило Лопиталя

Задача 9
Найти предел, используя правило Лопиталя.
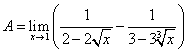
Решение
Неопределённость типа![]() приведём к виду
приведём к виду ![]() и используем правило Лопиталя
и используем правило Лопиталя

Задача 10
Функцию у = f(x) разложить ли формуле Тейлора и окрестности точки x0 до ![]()
![]()
![]()
![]()
Решение
Преобразуем к виду
![]()
Делаем замену х-2=t, х=t+2
![]()
Используем стандартные разложения
![]()
![]()
И формулу ![]()
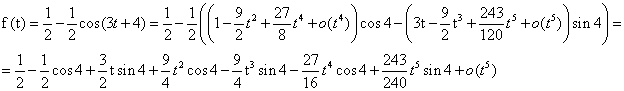 Возвращаемся к переменной х:
Возвращаемся к переменной х:
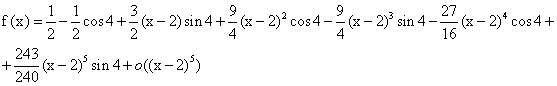
Задача 11
Вычислить предел двумя способами:
А) используя разложение по формуле Тейлора:
Б) с помощью правила Лопиталя.
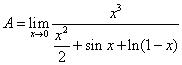
Решение
А)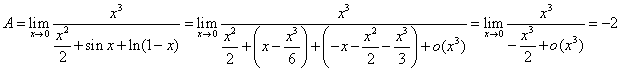
Б) 
Задача 12
Построить график функции ![]()
A=1, b=3, c=3, d=1, p=-2, q=1.
Решение
Исследуем функцию, заданную формулой: ![]()
Область определения: ![]()
Данная функция определена для:![]()
Решаем вспомогательное уравнение.![]() ,
, ![]()
Первая производная: 
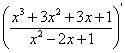 =
= =
=
= =
=
= =
=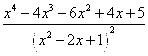
Вторая производная: 
Вторая производная это производная от первой производной.
 =
=
= =
=
= =
=
= =
=
= =
=
=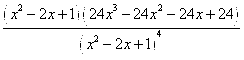 =
=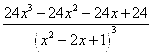
Точки пересечения с осью :
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
![]()
Дробь обращается в нуль тогда, когда числитель равен нулю.
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Точки пересечения с осью :
Пусть х=0 ![]()
Вертикальные асимптоты: х=1
Определим значения аргумента, при которых знаменатель функции обращается в ноль
![]() ,
, ![]()
Горизонтальные асимптоты: нет.
Наклонные асимптоты: у=х+5 .
Для нахождения наклонных асимптот преобразуем исходное выражение.
![]() =
=![]()
Предел разности исходной функции и функции х+5 на бесконечности равен нулю.
Критические точки: х=-1, х=5
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. 
Дробь обращается в нуль тогда, когда числитель равен нулю. ![]()
Решаем уравнение методом разложения на множители.
![]() ,
, ![]()
Случай. х+1=0, х=-1 Итак, ответ этого случая: х=-1.
Случай.![]() ,
,![]() ,
, ![]()
Случай. х-5=0, х=5 Итак, ответ этого случая: х=5.
Случай.![]() , Итак, ответ этого случая: х=1, х=-1.
, Итак, ответ этого случая: х=1, х=-1.
Итак, ответ этого случая: ![]() . не входит в ОДЗ функции.
. не входит в ОДЗ функции.
Возможные точки перегиба: х=-1
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. 
Дробь обращается в нуль тогда, когда числитель равен нулю.![]()
Следующее уравнение равносильно предыдущему. ![]() ,
, ![]() ,
,![]()
Случай.![]() ,
, ![]() Итак, ответ этого случая: х=1.
Итак, ответ этого случая: х=1.
Случай.![]() ,
, ![]() Итак, ответ этого случая:
Итак, ответ этого случая: ![]() .
.
не входит в ОДЗ функции.
Точки разрыва: х=1
Симметрия относительно оси ординат: нет ![]()
Симметрия относительно начала координат: нет ![]()
Тестовые интервалы:

Результаты исследования функции занесем в таблицу.
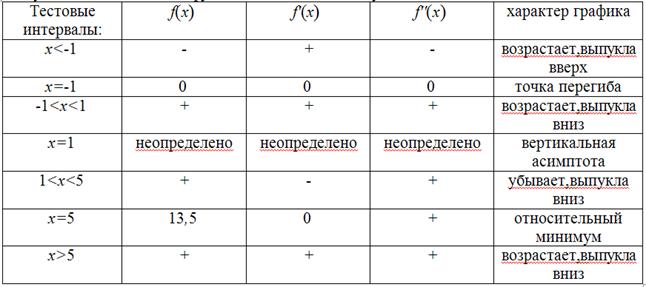
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум.
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
Множество значений функции: множество всех действительных чисел
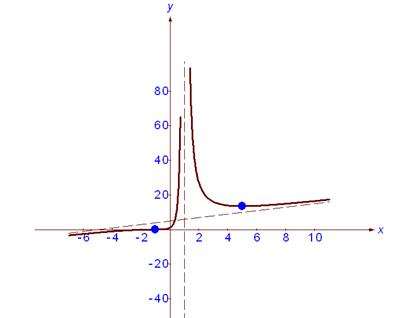
Рис. 1
Задача 13
Построить график функции ![]()
![]()
Решение
1). Область определения : ![]() .
.
2). Периодической функция не является
![]()
3). График не имеет вертикальних и горизонтальных асимптот.
Наклонная асимптота функции:
![]()
4). Пересечение с осью абсцисс (OX):
![]()
Пересечения графика с осью OY: ![]()
5). Поведение функции в граничных точках области определения:
![]()
Поведение функции на бесконечности:
![]()
6). Производная данной функции.
Производная функции равна:
![]()
Нули производной:
![]()
Функция возрастает на: ![]() . Функция убывает на:
. Функция убывает на: ![]()
7). С учётом предыдущих пунктов строим график функции y(x).
Строим график
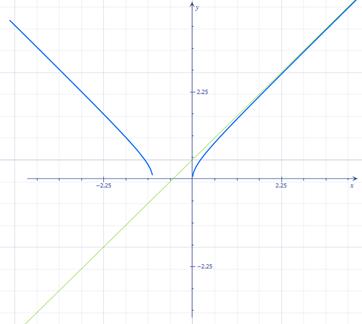
Рис. 2
Задача 14
Построить график функции
![]()
Решение
1). Область определения ![]() .
.
2). Периодической функция не является.
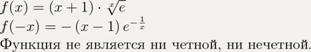
3). Наклонная асимптота функции: ![]()
4). Пересечение с осью OY: нет
Пересечения графика с осью OХ:
![]()
5). Поведение функции в граничных точках области определения:
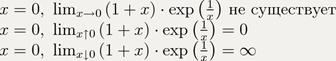
Поведение функции на бесконечности:
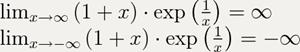
6). Производная данной функции равна
![]()
Определяем положение экстремумов. Решим уравнение ![]()
![]()
Функция возрастает на: ![]()
Функция убывает на: ![]()
7). С учётом предыдущих шести пунктов строим график функции y(x).
График функции приведён на рис. 3.
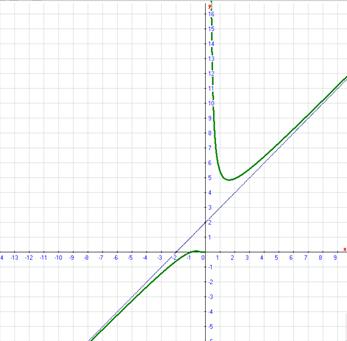
Рис. 3
Задача 15
Построить линию, заданную уравнением ![]() в полярных координатах
в полярных координатах ![]()
![]()
Решение
Преобразуем данную функцию к виду: ![]() . Период функции равен
. Период функции равен ![]() . Если вместо
. Если вместо ![]() подставить
подставить ![]() , то уравнение не изменится. Отсюда следует, что кривая симметрична относительно полярной оси. График состоит из 4х лепестков. Вычислим значения функции
, то уравнение не изменится. Отсюда следует, что кривая симметрична относительно полярной оси. График состоит из 4х лепестков. Вычислим значения функции ![]() , подставляя значения нескольких углов
, подставляя значения нескольких углов ![]() . Получим:
. Получим:

На рис. 4 приведён график.
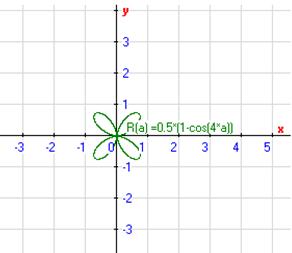
Рис. 4
Задача 16
Вычислить приближенно указанные величины.
![]()
Решение
Рассмотрим функцию ![]() . Выберем, соответственно,
. Выберем, соответственно, ![]() ,
, ![]() . Найдём значения функции и её производной:
. Найдём значения функции и её производной:
![]() ,
, ![]() ,
, ![]()
Используя формулу для приближённых вычислений, ![]() , получим:
, получим:
![]()
Задача 17
Вычислить приближенно указанные величины.
![]()
Решение
Рассмотрим функцию ![]() . Выберем, соответственно,
. Выберем, соответственно, ![]() ,
, ![]() . Найдём значения функции и её производной:
. Найдём значения функции и её производной:
![]() ,
, ![]() ,
, ![]()
Используя формулу для приближённых вычислений, ![]() , получим:
, получим:
![]()
Задача 18
Вычислить частные производные первого порядка
![]()
Решение
Вычисляем первые производные:
![]() ,
,![]()
Задача 19
Вычислить смешанные производные второго порядка и проверить, что они равны.
![]()
Решение
Вычисляем первые производные:
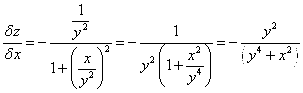 ,
, 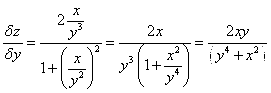
Дифференцируя первое равенство по y, а второе – по х, находим смешанные производные:


Убеждаемся, что равенство![]() выполнено
выполнено
Задача 20
Найти и исследовать точки экстремума функции.
![]()
Решение
Найдём стационарные точки из условия:
![]() ;
;
![]() ;
;
![]() .
.
Решая получившуюся систему уравнений, получим координаты стационарной точки ![]() :
: ![]() ,
, ![]() ,
, ![]() . В
. В ![]() выполнено необходимое условие экстремума. проверим выполнение достаточного условия экстремума. Проверим критерий Сильвестра. Вычислим в
выполнено необходимое условие экстремума. проверим выполнение достаточного условия экстремума. Проверим критерий Сильвестра. Вычислим в ![]() вторые производные.
вторые производные.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
И составим из них матрицу ![]()
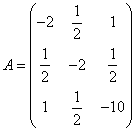
Угловые миноры матрицы А
![]()

![]()
Т. к. ![]() ,
, ![]()
![]() то в точке
то в точке ![]() функция
функция ![]() имеет локальный максимум.
имеет локальный максимум.
| < Предыдущая | Следующая > |
|---|