Глава 52. Производные основных элементарных функций

С помощью Определения производной, Правил дифференцирования, Теоремы о производной обратной функции и несложных математических преобразований легко получить Производные основных элементарных функций, которые мы сведем в одну таблицу производных. Пусть также – дифференцируемая функция, тогда

1. 

2. , .

3.  .

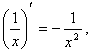
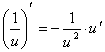4. , .

5. ,

6. ,

7. , .

8. , .

9.  (), .

10., .

11. , .

12. , .

13.  .

14. ,

15. .

16. , .

17. , .

18. , .

19. , .

20. , .

Формулы, приведенные выше вместе с правилами дифференцирования, являются Основными формулами дифференциального исчисления.

< Предыдущая		Следующая >