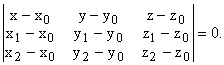Глава 31. Уравнение плоскости, проходящей через три точки. Уравнение плоскости в отрезках

Уравнение плоскости, проходящей через три точки

Если точки M0(x0;y0;z0), M1(x1;y1;z1), M2(x2;y2;z2) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

(2.17.1)

Пример

Написать уравнение плоскости, проходящей через три точки: M0(1;2;3), M1(2;1;2), M2(3;3;1).

Решение

Данные точки не лежат на одной прямой, так как векторы {1,–1,–1} и {2,1,–2} не коллинеарны. Плоскость M0M1M2 представляется уравнением 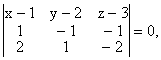т. е. x+z–4=0.

Уравнение плоскости в отрезках

Уравнение вида

А=D/A; B= D/B, C= D/A,

(2.17.2)

Называется Уравнением плоскости в отрезках, a, b и c –соответственно абсцисса, ордината и аппликата пересечения плоскости с осями Ox, Oy и Oz (рис. 2.17.1).

Рис. 2.17.1

Пример

Написать уравнение плоскости 3x – 6y +2z – 12 = 0 в отрезках.

Решение

Очевидно, что a=4, b=–2, c=6. Тогда уравнение плоскости в отрезках есть

< Предыдущая		Следующая >