2.4. Линии второго порядка

К линиям второго порядка относят окружность, эллипс, гиперболу и параболу.

Каноническое Уравнение окружности имеет вид

,

Где R- Радиус окружности.

Каноническое уравнение эллипса имеет вид

Где .

Каноническое уравнение гиперболы имеет вид

,

Где .

Каноническое уравнение параболы имеет вид

А) , где > 0 ( парабола симметрична относительно оси );

Б) (парабола симметрична относительно оси).

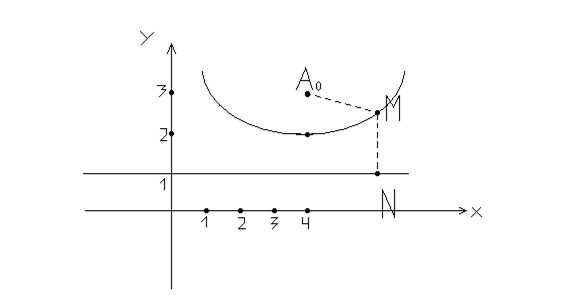
Задание 3. Составить уравнение линии, каждая точка которой одинаково удалена от точки и прямой . Сделать чертеж.

Решение Пусть М (X, Y) – любая точка искомой линии, - основание перпендикуляра, опущенного из точки на прямую Y. Тогда точка имеет координаты . Расстояние от точки М до прямой есть расстояние между точками М и N:

.

Теперь определим расстояние между точками М и :

.

По условию задачи . Следовательно, для любой точки справедливо равенство:

Или

.

Окончательно,

.

Полученное уравнение является уравнением параболы с вершиной в точке . Действительно, сделаем замену

.

Тогда уравнение примет вид:

(каноническое уравнение параболы ).

< Предыдущая		Следующая >