2.2. Элементы векторной алгебры и аналитической геометрии в пространстве

Любой вектор в декартовой системе координат может быть представлен в виде

Где координаты вектора Орты координатных осей.

Вектор с началом в точке и концом в точке Имеет вид:

,

то есть .

Длина отрезка называется Длиной (модулем) вектора, обозначается = и вычисляется по формуле

.

Сумма векторов и определяется формулой

Произведение вектора На число определяется формулой

.

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т. е.

.

Скалярное произведение векторов и вычисляется по формуле:

.

Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:

1) длина вектора равна площади параллелограмма, построенного на векторах и , т. е. ;

2) вектор перпендикулярен векторам и ;

3) векторы образуют правую тройку, то есть они ориентированы по отношению друг к другу соответственно как орты .

Модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на этих векторах:

Векторное произведение векторов и вычисляется по формуле:

.

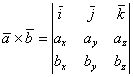Смешанным произведением векторов называется скалярное произведение вектора на вектор , то есть .

Модуль смешанного произведения векторов численно равен объему параллелепипеда, построенного на этих векторах:

Пусть Тогда

.

Уравнение любой плоскости может быть записано в виде:

где .

Вектор , перпендикулярный плоскости, называется Нормальным Вектором плоскости.

Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

Угол между плоскостями и определяется следующим образом:

.

Расстояние от точки До плоскости, определяемой уравнением , находится по формуле

.

Прямая В пространстве может быть задана уравнениями двух плоскостей

,

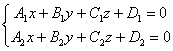Пересекающихся по этой прямой, или Каноническими уравнениями прямой

,

Которые определяют прямую, проходящую через точку и параллельную вектору . Вектор называется Направляющим вектором прямой.

Уравнения прямой, проходящей через две точки и , имеют вид:

.

Угол между Двумя прямыми и определяется следующим образом:

.

Угол между прямой и плоскостью определяется следующим образом:

.

Если Точка Делит отрезок АВ, где ,, в Отношении, то координаты точки М определяются по формулам:

.

Задание 1. Даны координаты вершин пирамиды : , . Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Решение. 1) Для определения длины ребра найдем координаты вектора : . Тогда длина ребра будет равна длине вектора :

.

2) Найдем угол между ребрами и . Для этого, как и раньше, найдем координаты вектора , определяющего ребро . Получим и .

Тогда угол между ребрами и можно найти из определения скалярного произведения двух векторов:

.

Следовательно, .

3) Чтобы найти угол между ребром и гранью , определим нормальный вектор Плоскости . Из определения векторного произведения двух векторов имеем:

,

Т. е. и . Тогда , .

Так как нормальный вектор перпендикулярен плоскости , то угол между ребром и гранью определяется как .

4) Площадь грани можем найти по формуле . Следовательно, Кв. ед.

5) Объем пирамиды, построенной на векторах, равен 1/6 объема параллелепипеда, построенного на этих же векторах. Для определения объема параллелепипеда воспользуемся свойством смешанного произведения векторов. В результате имеем:

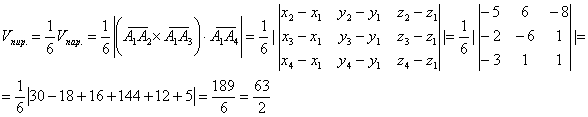Таким образом, куб. ед.

6) Составим уравнения прямой . Для этого воспользуемся уравнениями прямой, проходящей через две заданные точки И :

.

Получаем:

.

7) Уравнение плоскости можно найти по формуле:, где , . Следовательно, уравнение плоскости имеет вид: или после упрощения .

8) Чтобы составить уравнение высоты , опущенной из вершины на грань , воспользуемся формулой:

,

Где , - направляющий вектор высоты Пирамиды . Так как вектор Перпендикулярен грани , то в качестве Можно взять вектор - нормальный вектор плоскости .

Следовательно, имеем: или .

9) Сделаем теперь чертеж:

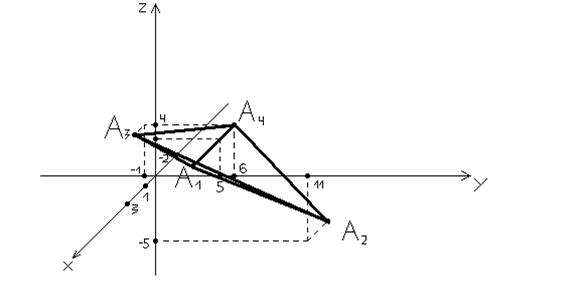
< Предыдущая		Следующая >