1.3.2. Матричный способ решения системы линейных алгебраических уравнений

Систему (1) можно записать в матричном виде

,

Где

, , .

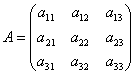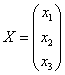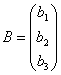Если определитель матрицы А отличен от нуля, то система (1) совместна и имеет единственное решение, определяемое формулой , где - матрица, обратная к А.

Задание 3. Дана система:

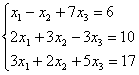(2)

Решить ее двумя способами:

1) по формулам Крамера

2) матричным способом

Решение

1. Вычислим определитель системы (2):

.

, следовательно, система (2) совместна и имеет единственное решение. Находим его, используя формулы Крамера:

, , ,

, , .

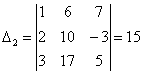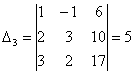2. Перепишем систему (2) в виде, Где

, , .

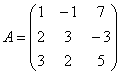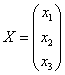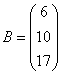Решение системы ищем в виде , где - матрица, обратная к А. Найдем (см. задание 2):

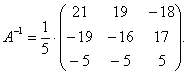
Следовательно,

,

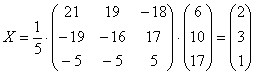Т. е. , , .

< Предыдущая		Следующая >