28. Свойства и применение определенных интегралов. Некоторые свойства определенных интегралов

Аддитивность (Рис. 17.1): .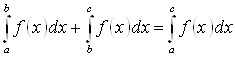

Интеграл от функции, имеющий произвольный знак (Рис. 17.2). При построении интегральных сумм знак функции не имеет значения. Определение интеграла без изменений распространяется на функцию , имеющую произвольный знак. В этом случае интеграл дает площадь криволинейной трапеции от до с минусом, а от до ‑ с плюсом. В результате мы получаем разность этих величин.

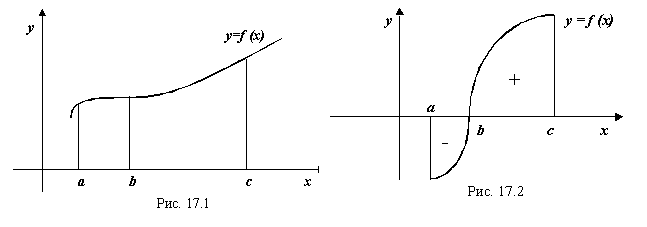Перемена пределов интеграла (Рис. 17.3). Целесообразно определить интеграл 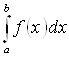и в случае, когда . Получаем .

Если , то .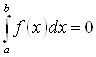

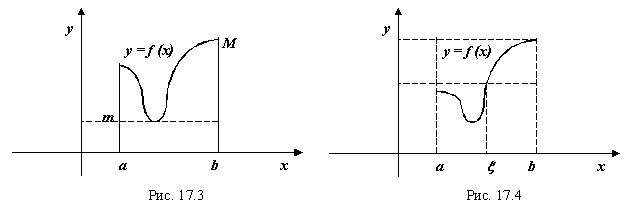
Теорема о среднем значении (Рис. 17.4). значение интеграла заключено между и , где и ‑ минимальное и максимальное значения функции на отрезке соответственно. Все интегральные суммы заключены в этих границах, а следовательно и интеграл: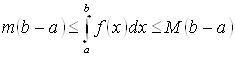

Если функция непрерывна, то внутри интервала существует такая точка , в которой функция принимает значение 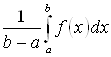. Следовательно, .

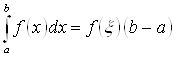Этот факт называют теоремой о среднем значении.

< Предыдущая		Следующая >