44. Непрерывные игры с выпуклыми функциями выигрышей

Напомним определение выпуклой функции G(X) действительной переменной X, которая определена на интервале (B, D).

Функция G(X) называется выпуклой (выпуклой вниз), если для любых точек X1, X2 из интервала (B, D) выполняется неравенство

, (4.11)

Где a1 и a2 – неотрицательные числа, причем a1 + a2 = 1.

График выпуклой функции G(X), представляет собой дугу, расположенную ниже хорды, стягивающей ее концы.

Функция G(X) называется вогнутой (выпуклой вверх), если для любых точек X1, X2 из интервала (B, D) вместо неравенства (4.11) выполняется неравенство

. (4.12)

Из определений выпуклой и вогнутой функций следует, что если функция G(X) вогнута (выпукла), то функция –G(X) соответственно является выпуклой (вогнутой) и наоборот. Это свойство позволяет ограничиваться рассмотрением только выпуклых функций и, соответственно, только выпуклых игр.

Если a1 ¹ 0 и a2 ¹ 0, то неравенства (4.11) и (4.12) превращаются в строгие неравенства и функция G(X) называется соответственно строго выпуклой или строго вогнутой.

Аналогичным образом вводится выпуклость для функции N переменных G(X1, X2, ¼, Xn), которая определена и непрерывна на некоторой замкнутой области D. Функция G(X1, X2, ¼, Xn) выпукла на области D, если для любых двух точек , этой области выполняется неравенство

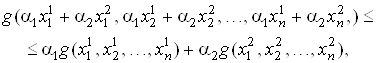(4.13)

Где a1, a2 ≥ 0 и a1 + a2 = 1.

Если a1 ¹ 0 и a2 ¹ 0 и неравенство (4.13) является строгим, то функция G(X1, X2, ¼, Xn) называется строго выпуклой на области D.

Для решения непрерывных игр с выпуклыми функциями важно, что непрерывная и строго выпуклая функция на замкнутой области определения D принимает только одно минимальное значение.

Введем теперь понятие непрерывной игры с выпуклой функцией выигрышей.

По-прежнему будем рассматривать бесконечную игру как тройку (X, Y, M(X, Y)), где множества X и Y являются единичными интервалами [0, 1], а функция M(X, Y) непрерывна на единичном квадрате [0, 1] ´ [0, 1]. Предположим также наличие у функции M(X, Y) достаточного числа непрерывных производных по X и Y .

Определение. Игра (X, Y, M(X, Y)) называется обобщенно-выпуклой, если существует такое целое число N > 0, что выполняется неравенство

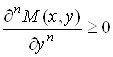, 0 £ x, Y £ 1, (4.14)

Или существует такое целое число M > 0, что имеет место неравенство

, 0 £ x, Y £ 1. (4.15)

При N = 2 или (и) M = 2 имеем выпуклые игры. Неравенство (4.14) в этом случае означает, что функция M(X, Y) является выпуклой функцией по Y при всех значениях X. Соответственно из неравенства (4.15) следует, что функция M(X, Y) является вогнутой функцией по X при всех значениях Y.

Для определения решений выпуклых игр удобно использовать следующие две теоремы.

Теорема 4.2. Пусть игра (X, Y, M(X, Y)) имеет непрерывную по обоим аргументам функцию выигрышей M(X, Y) на единичном квадрате, которая строго выпукла по Y для любого X Î [0, 1]. Тогда второй игрок имеет единственную оптимальную чистую стратегию Y0 Î [0, 1], которая определяется из решения уравнения

, (4.16)

Где V – цена игры, определяемая из выражения

. (4.17)

Теорема 4.3. Пусть игра (X, Y, M(X, Y)) имеет непрерывную по обоим аргументам функцию выигрышей M(X, Y) на единичном квадрате, которая строго вогнута по X для любого Y Î [0, 1]. Тогда первый игрок имеет единственную оптимальную чистую стратегию X0 Î [0, 1], которая определяется из решения уравнения

, (4.18)

Где V – цена игры, определяемая из выражения

. (4.19)

Пример 4.4. Решить игру на единичном квадрате (X, Y, M(X, Y)) = ([0, 1], [0, 1], ). Определим последовательно первую и вторую производную функции M(X, Y):

;

, при 0 £ X, Y £ 1.

Поскольку вторая производная отрицательна при X Î [0, 1] и Y Î (0, 1), то функція строго вогнута и, следовательно, имеет экстремум в виде максимума. Цена игры находится по соотношению (4.19) теоремы 4.3

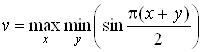. (4.20)

Второй игрок стремится минимизировать цену игры, поэтому при 0 £ X £ 0,5 он должен выбирать чистую стратегию Y = 0, в этом случае цена игры не будет превышать значения . При 0,5 £ X £ 1 для минимизации цены игры второй игрок должен выбирать чистую стратегию Y = 1. В этом случае первый игрок также не сможет выиграть больше . Поэтому выражение (4.20) можно преобразовать следующим образом

Максимальные значения обоих выражений под знаком функции максимума достигаются при X = X0 = 0,5. Поэтому имеем

.

Это же значение оптимальной чистой стратегии получается и с помощью выражения (4.18)

.

Или

. (4.21)

Поскольку минимум функции достигается при Y = 0, то из выражения (4.21) имеем и X = 0,5.

< Предыдущая		Следующая >