35. Признаки нулевых вероятностей применения чистых стратегий в смешанных
Пример 3.8. Рассмотрим матричную игру с матрицей
.
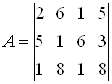Сопоставление первой и второй, первой и третьей стратегий первого игрока показывает, что часть элементов второй стратегии (первый и третий) доминируют соответствующие элементы первой стратегии, а те элементы первой стратегии, которые не доминируются элементами второй стратегии, доминируются элементами третьей стратегии: 5 > 2; 8 > 6; 6 > 1; 8 > 5. В связи с этим возникает предположение о том, что, быть может, первую стратегию первому игроку применять не выгодно, поскольку применение линейной комбинации его второй и третьей стратегий дадут ему больший выигрыш, чем применение первой стратегии. Поэтому полезно иметь простые признаки, позволяющие уменьшить размерность матрицы матричной игры, если одна из стратегий игрока уступает линейной комбинации двух или большего числа его других стратегий.
Определение. Выпуклой называется линейная комбинация l1X1 + l1X1 + ¼ + lNXn элементов X1, X2, ¼, Xn действительно векторного пространства (линейного пространства), в котором lK ³ 0, 
и 
.
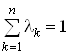Первый признак нулевой вероятности применения чистых стратегий в смешанных.
Если некоторая чистая стратегия K подчинена выпуклой линейной комбинации двух других чистых стратегий L и R, то подчиненная чистая стратегия K входит с нулевой вероятностью в смешанную стратегию.
Доказательство. Вначале рассмотрим этот признак применительно к первому игроку. Допустим, что существует матричная игра порядка N ´ M, чистые стратегии K, L и R первого игрока и число l (0 £ l £ 1), такие, что
, 
. (3.37)
Иначе говоря, стратегия K подчинена выпуклой линейной комбинации стратегий L и R. Тогда для любой смешанной стратегии второго игрока 
имеем
, 
(3.38)
Сложив неравенства (3.38), получим
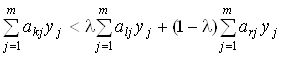. (3.39)
Поскольку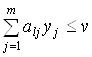 
, то из (3.39) получим
. (3.40)
Таким образом, стратегия K не обеспечивает первому игроку цены игры и, следовательно, ему нет смысла ее применять в своей смешанной стратегии.
Заметим, что в соотношениях (3.37) и (3.38) достаточно иметь только одно строгое неравенство, чтобы получить строгие неравенства в выражениях (3.39) и (3.40), поэтому в дальнейшем будем полагать, что неравенства (3.37) имеют вид
, , (3.41)
Где хотя бы одно из неравенств является строгим.
Доказательство признака для второго игрока выполняется аналогично. При этом соотношения вида (3.41) для второго игрока имеют вид
, 
, (3.42)
Где 0 < l < 1, L и R – стратегии второго игрока, доминирующие стратегию K.
Пример 3.9. Применим первый признак нулевой вероятности применения чистых стратегий в смешанных к матричной игре из примера 3.8
.
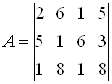Покажем, что первая стратегия первого игрока подчинена линейной выпуклой комбинации двух других его стратегий.
Запишем неравенства (3.41) для рассматриваемой игры:
2 £ 5l + 1(1 – l);
6 £ 1l + 8(1 – l);
1 £ 6l + 1(1 – l);
5 £ 3l + 8(1 – l).
Решим каждое из этих неравенств относительно l:
4l ³ 1, l ³ 0,25;
–7l ³ –7, l £ 1;
5l ³ 0, l ³ 0;
–5l ³ –3, l £ 0,6.
Итак, для l Î [0,25; 0,6] все неравенства (3.41) выполняются и действительно линейная комбинация второй и третьей стратегий превосходят первую стратегию, которая должна входить в смешанную стратегию с нулевой вероятностью.
Пример 3.10. Применить первый признак нулевой вероятности применения чистых стратегий в смешанных к стратегиям второго игрока в матричной игре
.
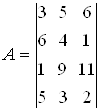Покажем, что вторая стратегия второго игрока подчинена линейной выпуклой комбинации его первой и третьей стратегий.
Неравенства (3.42) для рассматриваемого случая имеют вид:
3l + 6(1 – l) £ 5;
|
1l + 11(1 – l) £ 9;
5l + 2(1 – l) £ 3.
Решим каждое из этих неравенств относительно l:
–3l £ –1, l ³ 
;
5l £ 3, l £ 0,6;
–10l £ –2, l ³ 0,2;
3l £ 1, l £ .
Таким образом, при 
выполняются все неравенства (3.43), следовательно, линейная выпуклая комбинация первой и третьей стратегий второго игрока при 
превосходит его вторую стратегию.
Обобщение первого признака нулевой вероятности применения чистых стратегий в смешанных.
Если некоторая чистая стратегия K подчинена выпуклой линейной комбинации Q других стратегий, то подчиненная чистая стратегия входит с нулевой вероятностью в смешанную стратегию.
Доказательство обобщенного признака аналогично доказательству признака при Q =2.
Второй признак нулевой вероятности применения чистых стратегий в смешанных.
Если выпуклая линейная комбинация двух чистых стратегий подчинена выпуклой линейной комбинации других двух чистых стратегий, то в подчиненной выпуклой комбинации стратегий существует по меньшей мере одна чистая стратегия, входящая в смешанную стратегию с нулевой вероятностью.
Доказательство. Вначале докажем этот признак применительно к первому игроку.
Путь выпуклая линейная комбинация стратегий K и L первого игрока подчинена выпуклой линейной комбинации R и S других двух стратегий
, 
, 
, 
, (3.44)
И хотя бы одно из неравенств (3.44) является строгим.
Умножая левую и правую части неравенств (3.44) на компоненты смешанной стратегии 
второго игрока, получим
, 
. (3.45)
Просуммировав J полученных неравенств и учитывая, что хотя бы одно из неравенств (3.45) является строгим, имеем
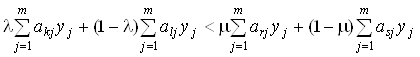. (3.46)
По теореме 3.3 имеем
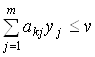и 
.
Положим, что 
и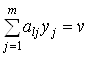 
, тогда неравенство (3.46) преобразуется к виду
. (3.47)
Поскольку по теореме 3.3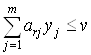 
и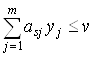 
, то правая часть неравенства (3.47) не может быть больше V, поэтому имеем V < V, т. е. приходим к противоречию. Следовательно, либо 
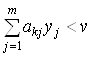, либо 
, либо выполняются оба этих неравенства, что и доказывает второй признак нулевой вероятности применения чистых стратегий в смешанных относительно первого игрока. Доказательство этого признака относительно второго игрока выполняется аналогично.
Признак несложно обобщить на произвольное число подчиненных или подчиняющих стратегий:
Если выпуклая линейная комбинация Q стратегий подчинена выпуклой линейной комбинации D других стратегий, то в подчиненной выпуклой линейной комбинации стратегий существует по меньшей мере одна чистая стратегия, входящая в смешанную стратегию с нулевой вероятностью.
Доказательство обобщенного признака аналогично доказательству признака при Q = D = 2.
| < Предыдущая | Следующая > |
|---|
