21. Синтез многокомпонентных критериев методом группового учёта аргументов
При наличии десятков или даже сотен различных показателей для принятия решений часто используются критерии вида:
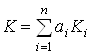 (2.1)
(2.1)
Или
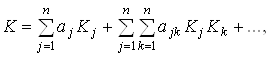 (2.2)
(2.2)
Где ![]() – весовые коэффициенты;
– весовые коэффициенты; ![]() – простейшие одно - или двухкомпонентные критерии.
– простейшие одно - или двухкомпонентные критерии.
Для получения критериев вида (2.1), (2.2) могут использоваться различные методы и алгоритмы. Рассмотрим один из них – алгоритм с линейными частными описаниями эвристического метода самоорганизации математических моделей (или метода группового учета аргументов (МГУА)), предназначенный для синтеза критериев вида (2.1). В этом алгоритме на первом этапе его работы в качестве простейших критериев или оценочных функций могут использоваться известные одно - или двухкомпонентные критерии: ![]() где верхний индекс указывает на то, что это критерии первого этапа или первого ряда селекции многокомпонентного критерия. При этом будем предполагать, что необходимо получить критерий K*, с помощью которого можно будет классифицировать множества некоторых объектов на два класса, например, объекты, обладающие некоторыми определенными свойствами (первый класс), и объекты, не обладающие этими свойствами (второй класс). Для синтеза критерия будем использовать обучающее множество M Объектов, для которых известна правильная классификация на два указанных класса M1 и M2, M1 Ç M2 = Æ, M1 È M2 = M. Рассмотрим основные шаги алгоритма синтеза критерия K*.
где верхний индекс указывает на то, что это критерии первого этапа или первого ряда селекции многокомпонентного критерия. При этом будем предполагать, что необходимо получить критерий K*, с помощью которого можно будет классифицировать множества некоторых объектов на два класса, например, объекты, обладающие некоторыми определенными свойствами (первый класс), и объекты, не обладающие этими свойствами (второй класс). Для синтеза критерия будем использовать обучающее множество M Объектов, для которых известна правильная классификация на два указанных класса M1 и M2, M1 Ç M2 = Æ, M1 È M2 = M. Рассмотрим основные шаги алгоритма синтеза критерия K*.
| < Предыдущая | Следующая > |
|---|