08. Свойства размещений и перестановок

Рассмотрим задачи, связанные со свойствами размещений и перестановок.

Пример 6.1. Вычислить

.

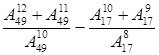Решение. Поскольку

И

,

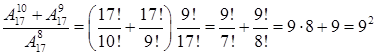То

.

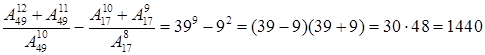Пример 6.2. Упростить выражение

(n ³ 6).

Решение. Поскольку

, ,

,

,

То

.

Пример 6.3. Решить неравенство

.

Решение. Из условия задачи следует, что n³1 и nÎ¥. Поскольку

, ,

То

И данное в условии неравенство равносильно неравенству

.

Пусть n³2, тогда , т. е. 20<15. Противоречие, следовательно, n=1 не является решением данного неравенства.

Пусть n=1, тогда исходное неравенство равносильно следующему

,

Отсюда следует, что первоначальное неравенство имеет три решения:

N1=3, n2=4 и n3=5.

Упражнения

6.1. Вычислить: а) , б) .

Ответ: а) 46, б) 80.

6.2. Упростить: .

Ответ: .

6.3. Решить неравенство .

Ответ: .

6.4. Найти все натуральные n, удовлетворяющие условию:

А) , б) , в) .

Ответ: а) 4, б) 4, в) 10.

6.5. Доказать, что .

< Предыдущая		Следующая >