05. Факториал
Для любого натурального числа n произведение ![]() обозначается n! (читается «эн факториал»), т. е.
обозначается n! (читается «эн факториал»), т. е.
![]()
Считается, что 0!=1.
Пример 3.1. Вычислить
 .
.
Решение. Так как ![]() и
и ![]() , то
, то
![]() .
.
Поскольку
![]() и
и ![]() ,
,
То
![]() .
.
Поэтому
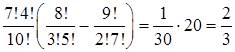 .
.
Пример 3.2. Упростить выражение
 (n³1).
(n³1).
Решение. Так как ![]() и
и ![]() , то
, то
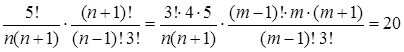 .
.
Пример 3.3. Решить уравнение
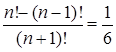 , где n³1.
, где n³1.
Решение. Так как ![]() , то
, то
![]() .
.
Кроме того, ![]() . Итак, исходное уравнение равносильно уравнению
. Итак, исходное уравнение равносильно уравнению
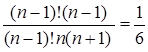 .
.
Если n=1, то уравнение примет вид
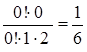 ,
,
Т. е. получается противоречие 0=1/6, следовательно, n=1 не является решением уравнения. Если n³2, то уравнение примет вид
 ,
,
Т. е. ![]() . Отсюда получаем n1=2 и n2=3.
. Отсюда получаем n1=2 и n2=3.
Выражение n! означает, что перемножаются все натуральные числа подряд и наибольший из сомножителей равен n. Выражение n!! означает, что перемножаются натуральные числа через одно и наибольший сомножитель также равен n. Таким образом, если n чётное, то n!! есть произведение всех чётных чисел, не превышающих n (![]() ); если же n нечётное, то это произведение всех нечётных чисел, не превышающих n (
); если же n нечётное, то это произведение всех нечётных чисел, не превышающих n (![]() ). Аналогично, если после числа расположено три восклицательных знака, то перемножаются каждое третье число, а если четыре – каждое четвёртое. Например,
). Аналогично, если после числа расположено три восклицательных знака, то перемножаются каждое третье число, а если четыре – каждое четвёртое. Например, ![]() .
.
Упражнения
3.1. Вычислить: а) ![]() , б)
, б) ![]() .
.
Ответ: а) ![]() , б)
, б) ![]() .
.
3.2. Упростить: а)  , б)
, б) 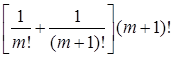
Ответ: а) ![]() , б) m+2.
, б) m+2.
3.3. Найти все натуральные n, удовлетворяющие условию 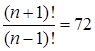 .
.
Ответ: 8.
3.4. В забеге участвуют 5 спортсменов. Сколькими способами могут распределиться места в результате забега?
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|