15. Формула включений и исключений

Принцип сложения можно применять в тех случаях, когда все множество перечисляемых комбинаций разбивается на попарно непересекающиеся группы комбинаций. Обобщим принцип сложения на случай, когда могут иметь место случаи непустых пересечений.

Пусть имеется n предметов, которые могут обладать двумя свойствами A и B. При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или обоими свойствами. Обозначим через n(A), n(B), n(AB) количество предметов, обладающих свойством A, свойством B, обоими свойствами. Тогда число предметов, обладающих хотя бы одним из указанных свойств, равно

. (13.1)

Появление третьего слагаемого связано с тем, что число предметов обладающих обоими свойствами при сложении n(A) и n(B) учитывались дважды (см. рис. 13.1).

Формула (13.1) является частным случаем более общей формулы:

(13.2)

Которую называют формулой перекрытий, или формулой включений и исключений. Чаще эту формулу записывают в следующем виде.

Обозначим символом свойство A, которым данные предметы не обладают. Тогда число предметов, не обладающих ни одним из указанных свойств, будет равно

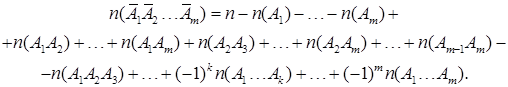(13.3)

Здесь алгебраическая сумма распространена на все комбинации свойств A1,…,Am (без учета их порядка), причем знак «+» ставится, если число учитываемых свойств четно, и знак «–», если это число нечетно. Название формулы (13.2) как формулы включений и исключений связано с тем, что сначала исключаются все предметы, обладающие хотя бы одним из свойств, потом включаются предметы, обладающие по крайней мере двумя из этих свойств, после этого исключаются предметы, обладающие по крайней мере тремя свойствами, и т. д.

В случае трёх свойств формулы (13.2) и (13.3) примут вид:

, (13.4)

. (13.5)

Пример 13.1. В научно-исследовательском институте работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык и 23 – оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?

Решение. Обозначим через A – сотрудников, знающих английский язык, через B – сотрудников, знающих немецкий язык. По условию

Тогда

.

Итак, 8 человек не знают ни английского, ни немецкого языка.

Пример 13.2. Сколько можно сделать перестановок из n элементов, в которых данные два элемента a и b не стоят рядом? Данные три элемента a, b, c не стоят рядом (в любом порядке)? Никакие два из элементов a, b, c не стоят рядом?

Решение. Если a и b стоят рядом, то их можно объединить в один знак. Учитывая, что a и b можно переставлять местами, получаем перестановок, в которых a и b стоят рядом. Тогда в

Случаях они не стоят рядом. Точно также получаем, что a, b, c не стоят рядом

Случаях. Никакие два из элементов a, b, c не стоят рядом

Случаях (формула включений и исключений).

Пример 13.3. Сколькими способами можно посадить рядом 3 англичан, 3 французов и 3 немцев так, чтобы никакие три соотечественника не сидели рядом?

Решение. 9 человек можно пересаживать 9! способами. Найдём, во скольких перестановках 3 англичанина сидят рядом. Все такие перестановки получаются из одной пересаживанием между собой англичан (3! способов) и 3 французов и 3 немцев и компании из трех англичан (7! способов). Всего получаем 3!7! перестановок. Во стольких же перестановках сидят рядом 3 французов и во стольких же – 3 немцев. Далее, в (3!)25! перестановках сидят рядом трое англичан и трое французов, а также трое англичан и трое немцев, трое французов и трое немцев. И, последнее, в (3!)4 перестановках сидят рядом и англичане, и французы, и немцы. В результате, по формуле включений и исключений, находим

способа.

Упражнения

13.1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек, и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?

Ответ: 25.

13.2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык, 6 человек знает английский язык, 6 – немецкий, 7 – французский, 4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?

Ответ: По формуле включений и исключений число работающих равно 6+7+6–4–3–2+1=11. Только английский знают 6–4–2+1=1, только немецкий 6–4–3+1=0, только французский 7–3–2+1=3. Т. о., только один язык знают 4 человека.

13.3. Староста одного класса дал следующие сведения об учениках: «В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом». Покажите, что в этих сведениях есть ошибка.

Ответ: Число школьников, которые не учатся на хорошо и отлично и не занимаются спортом, равно 45–30–28+17=4. Число мальчиков, которые не учатся на хорошо и отлично и не занимаются спортом, равно 25–16–18+15=6, т. е. их больше 4, что не может быть.

13.4. В лифт сели 8 человек. Сколькими способами они могут выйти на четырех этажах так, чтобы на каждом этаже вышел, по крайней мере, один человек?

Ответ: 8 пассажиров могут распределиться между этажами 48 способами. Из них в 38 случаях на данном этаже, 28 случаях на данных двух этажах и в 1 случае на данных трех этажах не выйдет ни один человек. По формуле включений и исключений получаем способа.

13.5. Сколько неотрицательных целых чисел, меньших чем миллион, содержит все цифры 1, 2, 3, 4? Сколько чисел состоит только из этих цифр?

Ответ: По формуле включений и исключений получаем, что все цифры 1, 2, 3, 4 содержат чисел. Только из цифр 1, 2, 3, 4 состоят чисел.

< Предыдущая		Следующая >