10. Свойства сочетаний
Отметим некоторые свойства сочетаний:
1. ![]() (свойство симметрии).
(свойство симметрии).
Например, ![]()
2. ![]() (свойство Паскаля).
(свойство Паскаля).
Данное равенство является рекуррентным соотношением для числа сочетаний. С помощью этого равенства можно составить таблицу для нахождения числа сочетаний. Расположим сочетания в виде треугольной таблицы
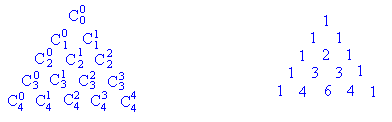
Полученную треугольную таблицу принято называть треугольником Паскаля.
3. ![]() .
.
Пример 8.1. Решить уравнение
![]() .
.
Решение. Поскольку ![]() , то получим квадратное уравнение
, то получим квадратное уравнение
![]() .
.
Учитывая, что ![]() , получаем решение
, получаем решение
![]() .
.
Пример 8.2. Решить неравенство
![]() .
.
Решение. Из условия задачи следует, что n³2 и nÎ¥. Поскольку
![]() ,
, ![]() ,
,
То
![]() .
.
Таким образом, исходное неравенство равносильно неравенству
![]() .
.
Поскольку при n=10 получаем ![]() , а при n=9 получаем
, а при n=9 получаем ![]() . Учитывая, что n³2 получаем
. Учитывая, что n³2 получаем
![]() .
.
Пример 8.3. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
Решение. Для звукосочетания клавиши нажимаются одновременно, поэтому для k звуков имеем ![]() звукосочетаний. Таким образом, искомое количество есть
звукосочетаний. Таким образом, искомое количество есть
![]() .
.
Учитывая свойство 3, т. е., что
![]() ,
,
Получим
![]() .
.
Упражнения
8.1. Вычислить: а) ![]() , б)
, б) 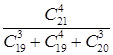 .
.
Ответ: а) 81, б) 1.
8.2. Упростить: 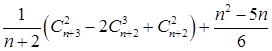 .
.
Ответ: 2.
8.3. Найти все натуральные n, удовлетворяющие условию:
А) ![]() , б)
, б)  .
.
Ответ: а) 3, б) 14.
8.4. Решить неравенство: а) ![]() , б)
, б) ![]() .
.
Ответ: а) ![]() , б)
, б) ![]() ,
,
8.5. Доказать, что ![]() .
.
8.6. Имеется 12 различных цветов. Сколькими способами можно составить букет из данных цветов, если в букет должно входить не менее 3 цветов?
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|