42. Поиск в глубину

Наш интерес к исследованиям Тремо объясняется тем обстоятельством, что этот метод непосредственно приводит к классической рекурсивной функции обхода графов: посетив конкретную вершину, мы помечаем ее специальной меткой, свидетельствующей о том, что она посещена, затем, в режиме рекурсии, мы посещаем все смежные с нею вершины, которые еще не были помечены. Этот метод носит название метода поиска в глубину (DFS - depth-firstsearch). Это один из наиболее важных алгоритмов, с которыми доведется столкнуться. Метод DFS обманчиво прост, поскольку в его основе лежит знакомая идея и его реализация не вызывает трудностей; фактически это очень гибкий и мощный алгоритм, который применяется для решения множества трудных задач обработки графов.

На рисунке 42 дается графическое представление процесса исследования лабиринта, для которого используются стандартные чертежи графа. Указанные рисунки служат иллюстрацией динамики рекурсивного метода DFS и его соответствия с исследованием лабиринта методом Тремо.

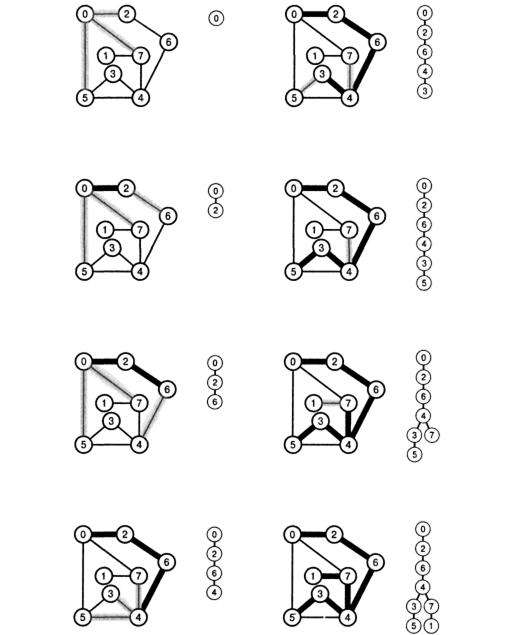
Рисунок 42

Данные диаграммы представляют собой графическое представление процесса поиска. Ребра графа, выделенные толстыми жирными линиями, соответствуют ребрам в дереве DFS, показанном справа от каждой диаграммы графа. Заштрихованные ребра — это ребра, намеченные для включения в дерево на следующих шагах. На ранних стадиях (слева) выполнения алгоритма дерево растет вниз в виде прямой линии, что соответствует рекурсивным вызовам для вершин 0,2, 6 и 4 (слева). Затем мы выполняем рекурсивные вызовы для вершины 3, затем для вершины 5 (справа, две верхних диаграммы), после чего возвращаемся из этих вызовов, чтобы сделать очередной рекурсивный вызов для вершины 7 из вершины 4 (справа, вторая снизу) и для 1 из 7 (справа снизу).

Подобно тому, как при обходе лабиринта мы дважды сталкиваемся с каждым коридором (по одному разу с каждого конца), так и в графе мы дважды сталкиваемся с каждым ребром (по одному разу в каждой его вершине). При проведении исследования Тремо мы открываем двери в обоих концах коридора. Применяя поиск в глубину к неориентированному графу, мы проверяем оба представления каждого ребра. Если мы встречаем ребро v-w, то либо совершаем рекурсивный поиск (если вершина w не помечена), либо пропускаем это ребро (если w помечена). Когда мы встретим это же ребро во второй раз, на этот раз с противоположной ориентацией, то есть w-v, мы его игнорируем, поскольку вершину назначения v мы уже определенно посещали (первый раз, когда сталкивались с этим ребром).

Одно из различий между поиском в глубину и исследованием Тремо заслуживает того, чтобы потратить некоторое время на его изучение, хотя во многих контекстах оно не играет никакой роли. Когда мы перемещаемся из вершины v в вершину w, мы не проверяем никаких ребер, ведущих из вершины w в другие вершины графа. В частности, мы знаем, что существует ребро из v в w и оно будет проигнорировано, когда мы на него выйдем (поскольку v помечена как посещенная вершина). Подобное решение приходится принимать в моменты, которые отличаются от ситуаций, имеющих место во время проведения исследований Тремо, когда мы открываем дверь, соответствующую ребру, идущему из v в w, когда мы попадаем в вершину w из v в первый раз. Если бы мы закрывали эти двери во время входа и открывали во время выхода (обозначив соответствующий коридор за счет протягивания вдоль него нити), то в этом случае мы бы имели точное соответствие между поиском в глубину и исследованием Тремо.

Алгоритм поиска в глубину посещает все ребра и все вершины, связанные с исходной вершиной, независимо от того, в какой последовательности он проверяет ребра, инцидентные каждой вершине. Этот факт есть прямое следствие свойства 6.1, поскольку доказательство этого свойства не зависит от порядка, в каком двери открываются на любом заданном перекрестке.

< Предыдущая		Следующая >