38. Планарность и двойственность. Планарные графы

Будем говорить, что граф укладывается на поверхности S, если его можно так нарисовать на S, что никакие два его ребра не пересекаются. Граф называется планарным, если его можно уложить на плоскости; плоский граф — это граф, уже уложенный на плоскости. Например, кубический граф, показанный на рисунке 35а, планарный, поскольку он изоморфен плоскому графу, изображенному на рисунке 35б.

Рисунок 35 (а, б)

Очевидно, что если граф имеет петли или параллельные ребра, то ни в какой из его планарных укладок нельзя изобразить все ребра в виде отрезков прямых линий. Здесь, естественно, возникает вопрос: для каждого ли планарного графа G существует укладка, в которой все ребра могут быть изображены в виде отрезков прямых? Как устанавливается в следующей теореме, ответ на данный вопрос – положительный.

Теорема 4. Для каждого простого планарного графа существует планарная укладка, в которой все ребра графа можно изобразить в виде отрезков прямых линий.▪

Если граф не укладывается на плоскости, то его можно уложить на некоторой другой поверхности. Покажем, что укладываемость графа на плоскости и на сфере эквивалентны, т. е. если граф укладывается на плоскости, то он укладывается на сфере, и наоборот. В доказательстве этого утверждения используется понятие так называемой стереографической проекции сферы на плоскость, описываемое ниже.

Допустим, что мы положили сферу на плоскость. Назовем точку соприкосновения южным полюсом, а диаметрально противоположную точку на сфере — северным полюсом N. Пусть P — произвольная точка на сфере. Тогда точка Р', в которой прямая, соединяющая точки N и Р пересекает плоскость, называется стереографической проекцией точки P на плоскости. Очевидно, что между точками на сфере и их стереографическими проекциями на плоскости существует взаимно-однозначное соответствие.

Теорема 5. Граф G укладывается на плоскости тогда и только тогда, когда он укладывается на сфере.

Доказательство. Пусть G' — укладка графа G на сфере. Положим сферу на плоскость так, чтобы северный полюс не был ни вершиной, ни точкой на ребре укладки G'.

Тогда образ G' в стереографической проекции — это укладка графа G на плоскости, поскольку ребра укладки G' пересекаются только в своих концевых вершинах, а между точками на сфере, и их образами в стереографической проекции существует взаимно однозначное соответствие. Обратное доказывается аналогично. ▪

Два основных непланарных графа, называемые графами Куратовского, представлены на рисунке 36. Один из них К5 — полный граф на пяти вершинах, а другой — К3,3. Называем эти графы основными непланарными графами потому, что они играют основополагающую роль в характеризации планарности.

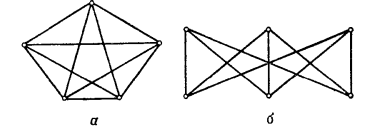
Рисунок 36 (а – К5, б – К3,3)

< Предыдущая		Следующая >