34. Орграфы и матрицы

Матрицей смежностей А(D) орграфа D называется (р×р)-матрица ||aij||, у которой aij= 1, если ViVj - дуга орграфа D, и aij=0 в противном случае. Матрица смежностей которого имеет вид (рис. 26):

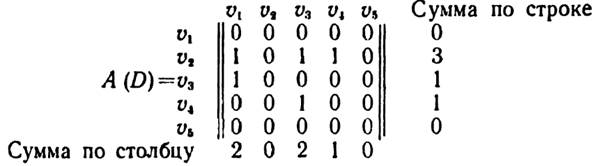
Рисунок 26

Легко проверить, что суммы элементов по строкам матрицы A(D) равны полустепеням исхода вершин орграфа D, а суммы элементов по столбцам - полустепеням захода.

Как и в случае графов, степени матрицы смежностей А орграфа дают полную информацию о числе маршрутов, идущих из одной вершины в другую. Теорема. (i, j)-й элемент аijn матрицы А" равен числу маршрутов длины n, идущих из вершины vi в вершину vj.

Упомянем здесь вкратце еще о трех матрицах, связанных с орграфом Ds - о Матрице достижимостей, Матрице расстояний и Матрице обходов. В матрице достижимостей R элемент rij равен 1,если вершина vi достижима из vj и равен 0 в противном случае. В матрице расстояний (i, j)-й элемент равен расстоянию из вершины vi в вершину vj; если же из vi в vj нет путей, то соответствующий элемент полагаем равным бесконечности. В матрице обходов (i, j)-й элемент равен длине наиболее длинного пути из vi в vj, а если таких путей нет, то опять-таки полагаем этот элемент равным бесконечности. Для орграфа D, показанного на рис. 27.

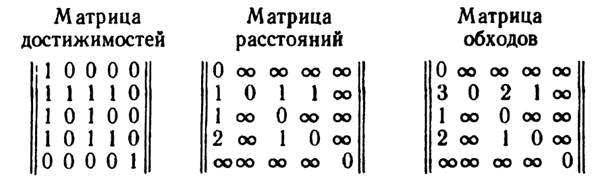
Рисунок 27

Следствие. Элементы матриц достижимостей и расстояний связаны со степенями матрицы А следующими соотношениями:

1) rii = 1 и dii = 0 для всех i;

2) rij = 1 тогда и только тогда, когда aijn> 0 для некоторого n;

3) d(vi, vj) равно наименьшему из чисел n, для которых aijn> 0

Эффективных методов для нахождения элементов матрицы обходов не существует. Эта проблема тесно связана с некоторыми другими давно поставленными алгоритмическими проблемами теории графов, такими, как нахождение остовных циклов и контуров, а также решение задачи о коммивояжере.

Поэлементное произведение В×С матриц B=||bij|| и C=||cij|| имеет своим (i, j)-м элементом bijcij. Матрицу достижимостей орграфа можно использовать для нахождения его сильных компонент.

< Предыдущая		Следующая >