21. Функция

Понятие «функции» является одним из основополагающих в математике. В дан­ном случае подразумеваются прежде всего функции, отображающие одно конеч­ное множество объектов в другое конечное множество. Мы избегаем использо­вания термина «отображение» и предпочитаем слово «функция» в расчете на постоянное сопоставление читателем математического понятия функции с поня­тием функции в языках программирования.

Пусть F — отношение из А в В, такое что

A (A,B) ϵF&(а, с) ϵFB = С.

Такое свойство отношения называется Однозначностью, Или Функциональностью, А само отношение называется Функцией из А в В И обозначается следующим образом: F:A→В. Если F: A→В, То обычно используется Префиксная Форма записи:

B = F(A)=(A,B) ϵF.

Если b = f(a), то а называют аргументом, а b — значением функции.

Пусть F:A→ В, тогда

Область определения Функции: FА= {AϵА | BϵВ B= F(а)};

Область значений функции: FB= {Bϵ В|АϵAb = F(а)}.

Если FА = A, то функция называется Тотальной, А если FА≠A — частичной. Сужением Функции F:A→ В на множество М А называется функция F|M, определяемая следующим образом:

F|M = {(а, b) | (а, b) ϵF& а ϵ М}

Для тотальной функции F= F|FA.

Функция F: A1×…× Ап→ В называется функцией N аргументов, Или П-местной Функцией.

Пусть F:A→ В. Тогда функция F называется:

Инъективной, ЕслиB = f(a1) & b = f(a2) A1 = a2;

Сюръективной, если Bϵ ВAϵА b = f(а);

Биективной, Если она инъективная и сюръективная.

Биективную функцию также называют Взаимнооднозначной.

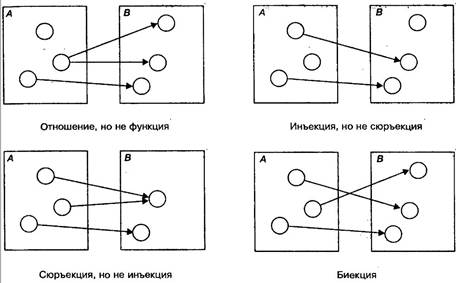
Следующий рисунок иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

Теорема. Если F:A→ В — тотальная биекция (FА = А), то отношение F -1В ×А (обратная функция) является биекцией.

Доказательство.

Поскольку F — биекция, имеем (B1= F (A)&B2 = F (A)B1 = B2) &(B= F(A1) &B = F (а2)A1 = A2) &(BϵВAϵА B = F(а)).

Покажем, что F -1 — Функция.

F -1 = {(b, а) | aϵА &bϵВ&b = f(а)}.

ПустьA1 = F -1(B) &а2 = F -1(B). ТогдаB= F(a1) &b = F (а2)A1 = A2.

Покажем, что F -1— инъекция. Пусть A1 = F -1(B1)& а2 = F -1(B2). Тогда B1= F (A)&B2 = F (A)B1 = B2.

Покажем от противного, что F -1— сюръекция.

Пусть AϵАBϵВ a = F -1(B). Тогда AϵАBϵВ a≠F -1(B). Обозначим этот элемент A0. Имеем Ba0≠f -1 (b) Bb≠F (A0) A0FAА→ A0А.

Пусть F:A→ В и пусть А1⊂ A, В1⊂В. Тогда множество

F(А1) = {Bϵ В |АϵА1B = F(а)}

Называется Образом Множества А1, а множество

F-1(В1) = { аϵ А |BϵВ1B = F(а)}

Прообразом Множества В1. Заметим, что FЯвляется отношением из множества 2FAВ множество 2FB:

F = {(Al, B1) | А1A& В1 В & В1= F(А1)}.

Теорема. Если F:A→ В Функция, тоF: 2FA→ 2FBИ F-1: 2FB→ 2FA– тоже функции.

F Называется Индуцированной Функцией, а F-1— Переходом к прообразам.

Принцип Дирихле. Пусть F:A→ В– функция, причем Х и Y – конечные множества. Если |Х|>то по крайней мере одно значение FВстретится более одного раза. Неформально, принцип Дирихле можно например записать следующим образом:

Если Х – множество белок, аY – множество клеток, и |Х| = 12, а |Y| =11, то 12 белок нельзя посадить в 11 клеток так, чтобы в каждой клетке находилась одна белка.

< Предыдущая		Следующая >