06. Примеры доказательств тождеств с множествами
Пример 1. Доказать или опровергнуть справедливость тождества(A
B)
C=(A
C)
(BC).
Доказательство. Докажем, используя метод взаимного включения. Пусть(AB)C=E, A(AC) (BC)=F.Тогда необходимо доказать или опровергнуть следующее:
E
F & FE.
1. Докажем необходимость: EF.
A
E
A(AB)C A(AB)& aC
(aA 
aB)& aC a(AC)
a( BC) 
a
(AC) (BC)⟹A∈F.
2. Докажем достаточность:FE
AFA(AC) (BC)A(AC) a( BC)(aA & aC)(aВ& aC) A(AB)& aC a
(AB)C⟹AE.
3. Следовательно, E=F, т. е. исходное тождество справедливо.
Пример 2. Доказать или опровергнуть справедливость тождества A
((AB)(AB))=
.
Доказательство. Докажем методом от противного: предположим, что это выражение не равно пустому множеству.
AA((AB)(AB))AA & a
((AB)(AB))AA & (a(AB)& a(AB))AA & (aA & aB) &(aA aB)
Получаем противоречие: элемент
одновременно принадлежит и не принадлежит множеству 
. Значит, первоначальное предположение неверно и исходное тождество справедливо, т. е. равно .
Пример 3. Доказать, чтоABB’A’.
Доказательство. Пусть А и В – подмножества некоторого универсума U, АB
XU, xA xB
XU, xA xB
XU, XB’ XA’
Значит B’ A’.
Пример 4.Доказать(AB)C=(AC) (BC).
Доказательство. Докажем, используя геометрический метод. Построим диаграммы Эйлера-Венна для множеств(AB)C И (AC) (BC):
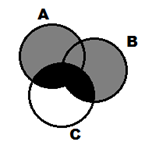
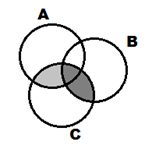
На первой диаграмме множество (AB)CВыделено черной штриховкой, на второй множество (AC) – светлой, множество (BC) – серой, а множество(AC) (BC)Является их объединением. Сравнивая эти два рисунка, можно сделать вывод, что эти множества равны, следовательно, тождество доказано.
| < Предыдущая | Следующая > |
|---|
