04. Операции над множествами

Объединением, двух множеств X и Y называется множество, обозначаемое XUY и состоящее из элементов, принадлежащих хотя бы одному из множеств X или Y:

XUY = {х | хϵ X или х ϵ Y}.

Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

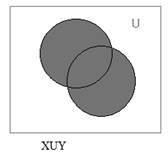
Пример. Рассмотрим два множества X = {1,3,5} и Y = {3,5,9}. Их объединением XUY будет множество {1,3,5,9}.

Пересечением, множеств X и Y называется множество, обозначаемое X∩Y состоящее из элементов, принадлежащих каждому из множеств X и Y:

X∩Y = {х | хϵ X и х ϵ Y}.

Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:

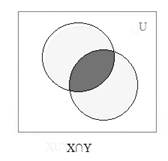
Пример. Рассмотрим два множества Х = {1,3,5} и Y= {3,5,9}. Тогда пересечением этих множеств будет X ∩Y = {3,5}.

Разностью множеств X и Y называется множество, обозначаемое X\Y и состоящее из всех элементов X, не принадлежащих Y:

X\Y = {х | хϵ X и х Y}.

Поясним определение разности множеств с помощью диаграммы Эйлера-Венна:

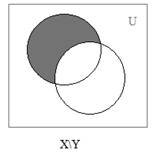
Пример. Рассмотрим два множества X = {1,3,5}, Y= {3,8,9}. Разностью этих множеств будет множество X\Y= {1,5}.

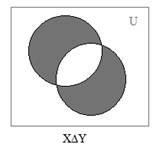
Симметричной разностью множеств X и Y называется множество

X∆Y = (X\Y)U(Y\X):

X∆Y = {х | (х ϵ X и х Y) и (х X и х ϵ Y)}.

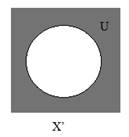
Дополнением к множеству Xотносительно универсального множества U называется множество X’ = U\X :

X’={X| XX}

Разбиением множества Y называется набор его Попарно непересекающихся подмножеств Xά, άϵ А, где А – некоторое множество индексов, такой, что Y = UXά, άϵ А.

Приоритет выполнения операций.

Сначала выполняются операции дополнения, затем пересечения, объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками. Если в выражении есть знаки пересечения и объединения и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).

< Предыдущая		Следующая >