61. Основы теории характеристических функций
Комплексная случайная величина Z определяется с помощью двумерной случайной величины (X, Y) следующим выражением
![]()
Операции над комплексными случайными величинами совпадают с операциями над комплексными числами.
Рассмотрим скалярную функцию случайных аргументов и числа i.
![]()
Тогда в теории вероятности математическое ожидание случайной величины вычисляется по тем же формулам, что и ![]() , просто i считают постоянным параметром.
, просто i считают постоянным параметром.
![]()
Найдем мат. ожидание случайной величины Z.
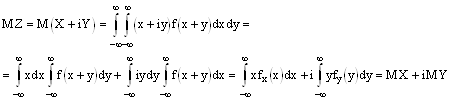
1. Для комплексной случайной величины справедливы свойства Аддитивности и Мультиплекативности мат. ожидания.

2. Комплексные случайные величины Z1 и Z2 называются Независимыми, если независимы между собой двумерные случайные величины ![]() , т. е. попарно независимы
, т. е. попарно независимы ![]()
Пусть Z1 и Z2 независимые комплексные случайные величины. Найдем мат. ожидание произведения

3. ![]()
А) дискретный случай

Б) непрерывный случай
Двумерная случайная величина XY имеет плотность вероятности f(x, y).

Характеристической функцией действительной случайной величины X называется функция
![]()
| < Предыдущая | Следующая > |
|---|