54. Многомерное нормальное распределение

N-мерная непрерывная случайная величина имеет нормальное распределение, если ее многомерная плотность вероятности в матричном виде

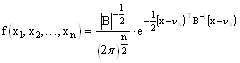
Показать, что формула

В двумерном случае переходит в

Для n=2 находим

Показатель степени при e

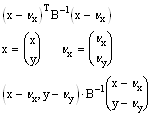
Найдем обратную матрицу матрице В

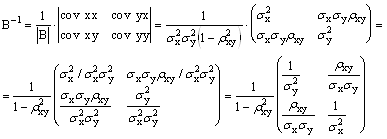
Проводим непосредственное доказательство

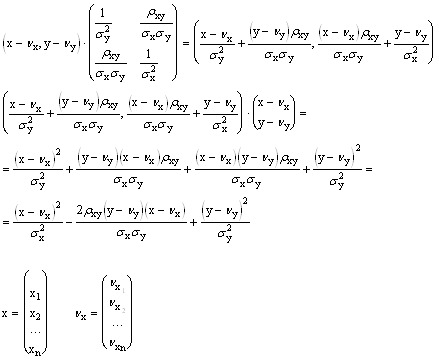
B - ковариационная матрица

Показать, что эта формула в двумерном случае совпадает с выражением, рассмотренном ранее.

Свойства n-мерного нормального распределения.

- определитель матрицы B - неотрицательное число.

По критерию Сильвестрова, если то все главные миноры матрицы B неотрицательные и определитель матрицы B неотрицателен.

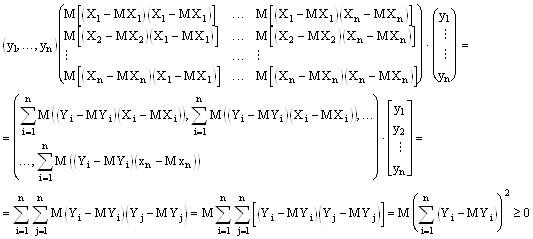
< Предыдущая		Следующая >